Phorum.com.gr

foscilis έγραψε: 03 Αύγ 2018, 13:36

sharp έγραψε: 03 Αύγ 2018, 13:33

Spiros252 έγραψε: 02 Αύγ 2018, 23:49 Η διατύπωση είναι δική μου παραλλαγή , ταυτόσημη όμως με την αρχική.

Η εκφώνηση θα μπορούσε να είναι θέμα εξετάσεων με στόχο να παραπλανήσει.

καλά σίγουρα θα τους γάμαγε, σαν πρόβλημα ασχολείται πιο πολύ με την έννοια της πιθανότητας (φιλοσοφικά) παρά με τα σχετικά μαθηματικά.

Κι εγώ αυτό πιστεύω. Αν το ερώτημα ήταν τύπου "αν ανοίξει την πόρτα κορίτσι, το άλλο παιδί θα είναι αγόρι ή κορίτσι;", "αν ανοίξει την πόρτα η γιαγιά τι πιθανότητα δίνετε στο να έχει δύο αρσενικά εγγόνια, δύο θηλυκά ή ένα από κάθε φύλο;", "αν ο Ζεβεδαίος είχε δύο παιδιά, τι φύλο ήταν τα παιδιά του;" κλπ δεν θα άλλαζε κάτι.

Παιδιά δεν είναι θέμα μαθηματικό. Στους υπολογισμούς των πιθανοτήτων γέννησης στη βιολογία, η πιθανότητα να βγει κορίτσι/αγόρι είναι ανεξάρτητη του αριθμού γεννήσεων και ανεξάρτητη της κληρονομικότητας. Την υπολογίζουμε πάντα 50% σε όλες τις ασκήσεις, ακριβώς, γιατί ο άντρας έχει ΧY, η γυναίκα ΧΧ και άρα όταν συνδυάζονται βγαίνουν ΧΧ,ΧΥ,ΧΧ, ΧΥ και συνεπώς, 50% να πάρεις ΧΧ (κορίτσι) και 50% να πάρεις ΧΥ (αγόρι) και αυτό σε κάθε γέννα.

ST48410 έγραψε: 03 Αύγ 2018, 01:30 Ναι, ωραία το εξηγείς. Μάλλον καταλαβαίνω τι λέτε.
Σπύρο να το πάρει το ποτάμι;

ΥΓ. Τι ωραίο πράγμα τα μαθηματικά! Διαφωνείς και σε ελάχιστο χρόνο σου εξηγεί ο άλλος και παραδέχεσαι την λύση και πάμε παρακάτω. Να μπορούσαμε να το κάνουμε και στην Εσωτερική πολιτική έτσι...

Το κλειδί της υπόθεσης - κατά τη γνώμη μου: Αν είναι τυχαίο ή όχι το ότι άνοιξε την πόρτα αγόρι.

Ακόμα κι αν ήξερε ο ερευνητής ότι στο σπίτι υπάρχει τουλάχιστον ένα αγόρι, πριν πάει, όταν θα άνοιγε την πόρτα ένα αγόρι, πάλι η πιθανότητα να είναι αγόρι και το άλλο θα μετατρεπόταν σε 1/2.

Cecily Anne έγραψε: 03 Αύγ 2018, 19:45 Παιδιά δεν είναι θέμα μαθηματικό. Στους υπολογισμούς των πιθανοτήτων γέννησης στη βιολογία, η πιθανότητα να βγει κορίτσι/αγόρι είναι ανεξάρτητη του αριθμού γεννήσεων και ανεξάρτητη της κληρονομικότητας. Την υπολογίζουμε πάντα 50% σε όλες τις ασκήσεις, ακριβώς, γιατί ο άντρας έχει ΧY, η γυναίκα ΧΧ και άρα όταν συνδυάζονται βγαίνουν ΧΧ,ΧΥ,ΧΧ, ΧΥ και συνεπώς, 50% να πάρεις ΧΧ (κορίτσι) και 50% να πάρεις ΧΥ (αγόρι) και αυτό σε κάθε γέννα.

Στο συγκεκριμένο πρόβλημα, οι πιθανότητες παίζαν στο αγόρι-αγόρι και αγόρι-κορίτσι. Το κορίτσι-κορίτσι, είχε φύγει. Εγώ έβαλα 4/5 αγόρι, γιατί στα κοριτσάκια αρέσει περισσότερο να ανοίγουν την πόρτα και έδωσα λιγότερες πιθανότητες στο να είναι η αδελφούλα μωρό.

Όταν δεν βρίσκω λογική βάση, χαλαρώνω και το διασκεδάζω.

Αυτο σπυ εξηγω δεν παίζονται εκει οι πιθανοτητες γιατι η καθε γεννά υπολογίζεται ξεχωριστά κ δεν εχει καμια σχεση με προηγούμενη η επόμενη .

Κάποιες ..λεπτομέρειες



https://www.npr.org/sections/health-sho ... 3315523774

Spiros252 έγραψε: 03 Αύγ 2018, 19:11

ritzeri έγραψε: 02 Αύγ 2018, 02:11 Η παρακατω διατύπωση του προβλήματος είναι ισοδύναμη με την αρχική;


"Ομάδα στατιστικής έρευνας επισκέπτεται τυχαία οικογένειες που έχουν ένα παιδί και η γυναίκα είναι έγκυος στο δευτερο.
Αν ο ερευνητής χτυπήσει την πόρτα και του ανοίξει ένα αγόρι, ποιά η πιθανότητα και το άλλο παιδί που θα γεννηθεί να είναι αγόρι;"

Ναι. Το ότι δεν έχει γεννηθεί ακόμα το παιδί δεν σημαίνει ότι δεν υπάρχει και δεν σημαίνει ότι δεν έχει φύλο.
Και υπάρχει και έχει συγκεκριμένο φύλο και βρίσκεται μέσα στο σπίτι.

Δεν νομίζω βρε Σπύρο.
Αλλάζουν τα δεδομένα.
Το πρόβλημα σε αυτή την περίπτωση θα γινόταν "αν ανοίξει την πόρτα το μεγαλύτερο παιδί και είναι αγόρι, τότε..."
Ενώ τώρα το αγόρι που θα ανοίξει μπορεί να είναι είτε το μεγαλύτερο είτε το μικρότερο παιδι

Spiros252 έγραψε: 03 Αύγ 2018, 19:54

ST48410 έγραψε: 03 Αύγ 2018, 01:30 Ναι, ωραία το εξηγείς. Μάλλον καταλαβαίνω τι λέτε.
Σπύρο να το πάρει το ποτάμι;

ΥΓ. Τι ωραίο πράγμα τα μαθηματικά! Διαφωνείς και σε ελάχιστο χρόνο σου εξηγεί ο άλλος και παραδέχεσαι την λύση και πάμε παρακάτω. Να μπορούσαμε να το κάνουμε και στην Εσωτερική πολιτική έτσι...

Το κλειδί της υπόθεσης - κατά τη γνώμη μου: Αν είναι τυχαίο ή όχι το ότι άνοιξε την πόρτα αγόρι.

Ακόμα κι αν ήξερε ο ερευνητής ότι στο σπίτι υπάρχει τουλάχιστον ένα αγόρι, πριν πάει, όταν θα άνοιγε την πόρτα ένα αγόρι, πάλι η πιθανότητα να είναι αγόρι και το άλλο θα μετατρεπόταν σε 1/2.

Δεν έχει σημασία αν άνοιξε τυχαία ή όχι το αγόρι.

Έστω ότι το ερώτημα γίνεται μετά την έρευνα.
Οι ερευνητές έστω ότι πήγαν σε 4000 σπίτια διτεκνων οικογενειών.
Στα 1000 άνοιξαν την πόρτα οι μπαμπάδες , στα 1000 οι μαμάδες , στα 1000 τα κορίτσια και στα υπόλοιπα 1000 τα αγόρια.
Από τα σπίτια αυτά τα 1000 που άνοιξαν την πόρτα τα αγόρια , τι ποσοστό μπλα μπλα μπλα

Dies Irae έγραψε: 03 Αύγ 2018, 20:14 Κάποιες ..λεπτομέρειες



https://www.npr.org/sections/health-sho ... 3315523774

παιζει πολυ σερνικοβοτανο στην κινα και την αρμενια σαν να λεμε

alekhine έγραψε: 03 Αύγ 2018, 20:26

Dies Irae έγραψε: 03 Αύγ 2018, 20:14 Κάποιες ..λεπτομέρειες



https://www.npr.org/sections/health-sho ... 3315523774

παιζει πολυ σερνικοβοτανο στην κινα και την αρμενια σαν να λεμε

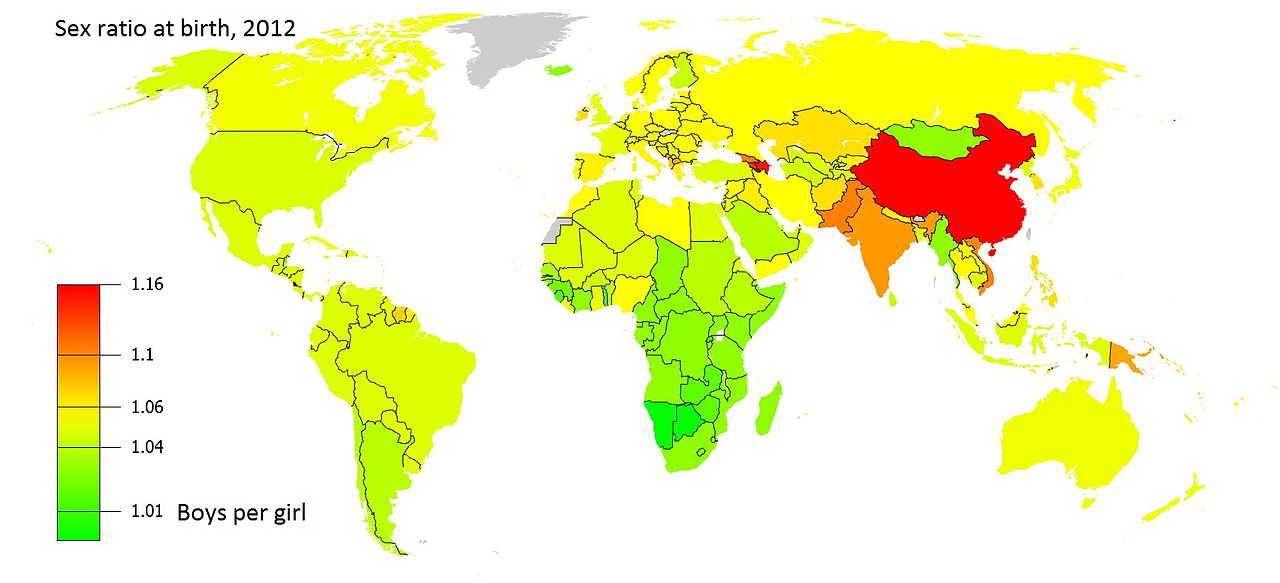
Για Κίνα (και για Ινδία), ..social factors( Sex-selective abortion δηλαδή)!

Κάτι είδα πριν εδώ:

https://en.m.wikipedia.org/wiki/Human_sex_ratio

Λέει και Αρμενία, Γεωργία, Αζερμπαϊτζάν

Cecily Anne έγραψε: 03 Αύγ 2018, 19:35 H κάθε γέννα υπολογίζεται με 50%. Και 15 παιδιά να έχεις, θα πρέπει να υπολογίσεις την κάθε γέννα με 50%.

δεν εστιάζει με το αν κάθε παιδί έχει 50% να ειναι αγόρι ή κορίτσι το πρόβλημα πάντως, το ξέρουμε οτι είναι 50-50.

αυτό το κάνει πιο απλό να δούμε την δυσκολία της ερώτησης

Αν ξέρεις οτι μία οικογένεια έχει δύο παιδιά, και ένα ειναι αγόρι αλλά δεν ξέρεις αν είναι το μεγάλο ή το μικρό, τι πιθανότητες έχεις και το δεύτερο να ειναι αγόρι;

εδώ η απάντηση ειναι 33%, όχι 50%.

ritzeri έγραψε: 03 Αύγ 2018, 20:19 Δεν έχει σημασία αν άνοιξε τυχαία ή όχι το αγόρι.

Από τα σπίτια αυτά τα 1000 που άνοιξαν την πόρτα τα αγόρια , τι ποσοστό μπλα μπλα μπλα

λάθος κάνεις νομίζω, αφού άνοιξαν τα αγόρια με το ζόρι δεν έχεις την τύχη μέσα, άνοιξαν σε 750 σπίτια και όχι 500, οπότε το ποσοστό ειναι 33%.

όπως και να ανοίξουν, από τα 1000 σπίτια τα 250 έχουν δύο αγόρια μέσα, τα 500 είναι μεικτά και τα άλλα 250 έχουν 2 κορίτσια. Είναι θέμα επιλογής, θα αφήσεις την τύχη να κάνει την διαίρεση, ή θα την κάνεις εσύ. Αν αφήσεις την τύχη, θα ανοίξουν 500 σπίτια, και τα μισά θα έχουν αγόρι, 50%. Αν δεν αφήσεις την τύχη, θα ανοίξουν όλα τα σπίτια που έχουν αγόρι, 750 δηλαδή, οπότε στο 1/3 θα έχεις δύο αγόρια, στο 33%.

ritzeri έγραψε: 03 Αύγ 2018, 20:16

Spiros252 έγραψε: 03 Αύγ 2018, 19:11

ritzeri έγραψε: 02 Αύγ 2018, 02:11 Η παρακατω διατύπωση του προβλήματος είναι ισοδύναμη με την αρχική;


"Ομάδα στατιστικής έρευνας επισκέπτεται τυχαία οικογένειες που έχουν ένα παιδί και η γυναίκα είναι έγκυος στο δευτερο.
Αν ο ερευνητής χτυπήσει την πόρτα και του ανοίξει ένα αγόρι, ποιά η πιθανότητα και το άλλο παιδί που θα γεννηθεί να είναι αγόρι;"

Ναι. Το ότι δεν έχει γεννηθεί ακόμα το παιδί δεν σημαίνει ότι δεν υπάρχει και δεν σημαίνει ότι δεν έχει φύλο.
Και υπάρχει και έχει συγκεκριμένο φύλο και βρίσκεται μέσα στο σπίτι.

Δεν νομίζω βρε Σπύρο.
Αλλάζουν τα δεδομένα.
Το πρόβλημα σε αυτή την περίπτωση θα γινόταν "αν ανοίξει την πόρτα το μεγαλύτερο παιδί και είναι αγόρι, τότε..."
Ενώ τώρα το αγόρι που θα ανοίξει μπορεί να είναι είτε το μεγαλύτερο είτε το μικρότερο παιδι

το ίδιο είναι, 50%, γιατί η τύχη πάλι λειτουργεί και φιλτράρει από το δείγμα τα σπίτια που θα έχουν κορίτσι-αγόρι, κοιτάμε μόνο αυτά που θα έχουν αγόρι-αγόρι ή αγόρι-κορίτσι. Και στην περίπτωση του μεγαλύτερου πάλι 50% είναι, ο μόνος τρόπος να πάει στο 33% είναι να ξέρεις σίγουρα ότι υπάρχει αγόρι, αλλά όχι αν είναι το πρώτο ή το δεύτερο.

Ωραίο προβληματάκι, μπορείτε να το βρείτε στην βιβλιογραφία ως 'Monty Hall' (στις διάφορες παραλλαγές)

Σε δύο παρεμβάσεις θέλω να σταθώ.

1.

Yochanan έγραψε: 02 Αύγ 2018, 08:54

Κώδικας: Επιλογή όλων

ProbBB <- function(N, Random){
  
  #test to see if random or known
  if (Random == TRUE)  {Shunt = 0}   else   {Shunt = 1}
  
  #Initialize variables    
  child<-c(0,0);marginal <- 0 ;joint <- 0
  for (i in 1:N){
    
    #assign values to vars from uniform dist
    child[1] = runif(1) ; child[2] = runif(1)  
    Test1 = runif(1)    ; Test2 = runif(1)
    
    #test to randomly make one of two always B (if known i.e. Random = 0)
    if (Test1 >= 0.5){child[1] <- child[1]+Shunt} else {child[2] <- child[2]+Shunt}
    
    #test to choose child to open door 
    if (Test2 >= 0.5) {Switch <- 0} else {Switch <- 1}
    
    #test to determine if child which opens door is B
    if (child[Switch+1] >= 0.5) { 
      marginal <- marginal + 1
      #test to determine if other child is also B given child that opens door is B
      if (child[(!Switch)+1] >= 0.5) { 
        joint <- joint + 1
      }
    }
  } 
ProbBB = 1-joint/marginal
}

Ο Γιοκ εδώ λύνει το πρόβλημα πρακτικά και οριστικά με προσωμοίωση, και οι αριθμοί δε λένε ψέμματα (συνήθως).
Αλλού όμως είναι το πόηντ.
Η R δεν είναι γλώσσα των πληβείων, είναι γλώσσα των Πατρικίων.
Γι' αυτό λοιπόν Γιοκ σνομπαρία δεν εμφανίστηκες ούτε μία φορά στο νήμα με τους μαθηματικούς γρίφους;
Τόσο πολύ θεωρείς ότι θα λεκιαστεί ο χιτώνας σου αν πάρεις μια γωνιά στο φόρουμ και μας παραθέσεις έναν-δύο κώδικες?
Τέτοια κάνεις και θα έχουμε προλεταριακές απαλλοτριώσεις αστικού τοπίου.












2.

Cecily Anne έγραψε: 03 Αύγ 2018, 19:45 Παιδιά δεν είναι θέμα μαθηματικό. Στους υπολογισμούς των πιθανοτήτων γέννησης στη βιολογία, η πιθανότητα να βγει κορίτσι/αγόρι είναι ανεξάρτητη του αριθμού γεννήσεων και ανεξάρτητη της κληρονομικότητας. Την υπολογίζουμε πάντα 50% σε όλες τις ασκήσεις, ακριβώς, γιατί ο άντρας έχει ΧY, η γυναίκα ΧΧ και άρα όταν συνδυάζονται βγαίνουν ΧΧ,ΧΥ,ΧΧ, ΧΥ και συνεπώς, 50% να πάρεις ΧΧ (κορίτσι) και 50% να πάρεις ΧΥ (αγόρι) και αυτό σε κάθε γέννα.

"Παιδιά δεν είναι θέμα μαθηματικό, και ορίστε η μαθηματική απόδειξη γι' αυτό"

enaon έγραψε: 03 Αύγ 2018, 20:43

Cecily Anne έγραψε: 03 Αύγ 2018, 19:35 H κάθε γέννα υπολογίζεται με 50%. Και 15 παιδιά να έχεις, θα πρέπει να υπολογίσεις την κάθε γέννα με 50%.

δεν εστιάζει με το αν κάθε παιδί έχει 50% να ειναι αγόρι ή κορίτσι το πρόβλημα πάντως, το ξέρουμε οτι είναι 50-50.

αυτό το κάνει πιο απλό να δούμε την δυσκολία της ερώτησης

Αν ξέρεις οτι μία οικογένεια έχει δύο παιδιά, και ένα ειναι αγόρι αλλά δεν ξέρεις αν είναι το μεγάλο ή το μικρό, τι πιθανότητες έχεις και το δεύτερο να ειναι αγόρι;

εδώ η απάντηση ειναι 33%, όχι 50%.

Σου απαντάω. Δεν αλλάζει η πιθανότητα ό,τι και να είναι το πρώτο. Το δεύτερο πάντα έχει 50% πιθανότητες να είναι αγόρι ή κορίτσι. Όπως και το τρίτο. Και δέκα κορίτσια να κάνει ένας το 11 πάλι έχει 50% να βγει αγόρι. Έτσι λύνονται όλες οι ασκήσεις Βιολογίας.

Χουργιατς έγραψε: 03 Αύγ 2018, 21:14

"Παιδιά δεν είναι θέμα μαθηματικό, και ορίστε η μαθηματική απόδειξη γι' αυτό"

Δεν είναι μαθηματική η απόδειξη, είναι βιολογική. Παίρνουν σαν δεδομένο ότι το χρωμόσωμα κληροδοτείται με 50% πιθανότητα. Αν είχαν απόδειξη για άλλο τρόπο κληρονομικότητας (πχ κάποιο υπολειπόμενο γονίδιο κλπ. θα άλλαζε το πράγμα).