Ωραίος!Ανίκητος έγραψε: 10 Φεβ 2025, 00:21 @pussycat
Spoiler
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
def simulate_joker_game(l_players, total_tickets, v=24435180, l=1):
"""
Simulates a Joker game where l_players each choose a random number of tickets
following a Poisson distribution with parameter l.
The tickets are collected and limited to total_tickets in size.
"""
# Generate random number of tickets for each player using Poisson distribution
#tickets_per_player = np.random.uniform(low=1, high=2*l, size=l_players).astype(int)
tickets_per_player = np.random.poisson(l, size=l_players)
#tickets_per_player = np.random.normal(loc=l, scale=l/2, size=l_players).astype(int)
tickets_per_player = np.maximum(tickets_per_player, 1) # Ensure at least 1 ticket per player
print("Sample of tickets per player:", tickets_per_player[:10])
print("Average number of tickets per player:", np.mean(tickets_per_player))
# Generate tickets chosen by players
all_tickets = np.concatenate([np.random.randint(1, v + 1, size=n) for n in tickets_per_player])
print("Sample of all generated tickets:", all_tickets[:10])
# Shuffle and not take only m (total_tickets) samples
np.random.shuffle(all_tickets)
ticket_list=all_tickets[:total_tickets]
print("Sample of final ticket list:", ticket_list[:10])
print("Ticket list size:", len(ticket_list))
# Count occurrences of each ticket
unique_tickets, frequencies = np.unique(ticket_list, return_counts=True)
# Print the number of unique tickets in the sample
print("Number of unique tickets in sample:", len(unique_tickets))
print("Winner probability:", len(unique_tickets)/v)
print("Average frequency of unique tickets:", np.mean(frequencies))
# Sort tickets by frequency in descending order
sorted_indices = np.argsort(frequencies)[::-1]
sorted_tickets = unique_tickets[sorted_indices]
sorted_frequencies = frequencies[sorted_indices]
print("Sample of sorted tickets:", sorted_tickets[:10])
print("Sample of sorted frequencies:", sorted_frequencies[:10])
return sorted_tickets, sorted_frequencies
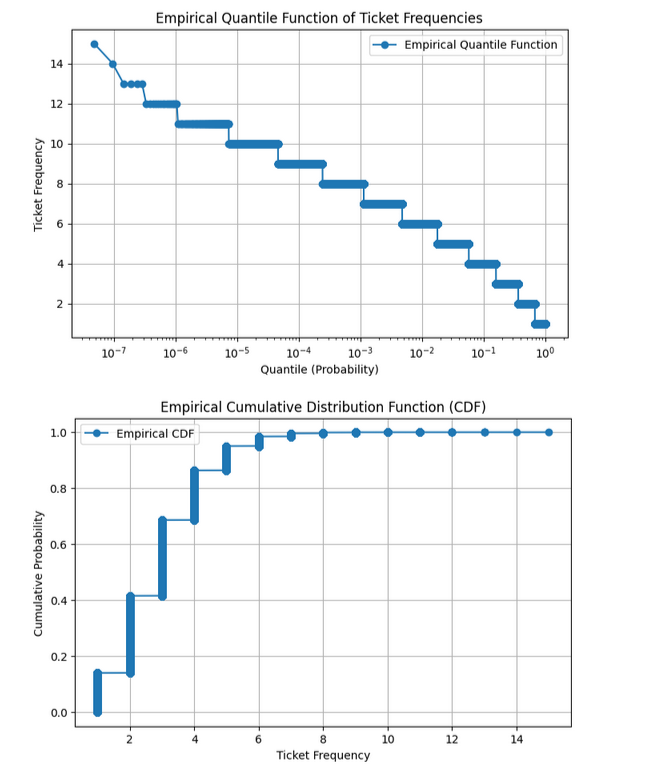
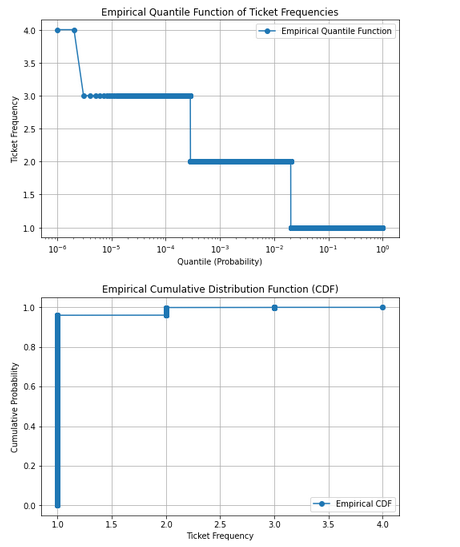
def plot_empirical_quantile(frequencies):
"""Plots the empirical quantile function from sorted frequencies."""
m = len(frequencies)
probabilities = np.linspace(1 / m, 1, m) # Percentile ranks
plt.figure(figsize=(8, 5))
plt.plot(probabilities, frequencies, marker="o", linestyle="-", label="Empirical Quantile Function")
plt.xscale("log")
plt.xlabel("Quantile (Probability)")
plt.ylabel("Ticket Frequency")
plt.title("Empirical Quantile Function of Ticket Frequencies")
plt.grid(True)
plt.legend()
plt.show()
def plot_empirical_cdf(frequencies):
"""Plots the empirical cumulative distribution function (CDF) from sorted frequencies."""
sorted_frequencies = np.sort(frequencies) # Sort frequencies in ascending order
ecdf = np.cumsum(sorted_frequencies) / np.sum(sorted_frequencies) # Normalize cumulative sum
plt.figure(figsize=(8, 5))
plt.plot(sorted_frequencies, ecdf, marker="o", linestyle="-", label="Empirical CDF")
plt.xlabel("Ticket Frequency")
plt.ylabel("Cumulative Probability")
plt.title("Empirical Cumulative Distribution Function (CDF)")
plt.grid(True)
plt.legend()
plt.show()
# Simulation Parameters
l_players = 48000000 # Number of players
total_tickets = 48000000 # The final collected ticket pool size
# Simulate the game
sorted_tickets, sorted_frequencies = simulate_joker_game(l_players, total_tickets)
# Plot the empirical quantile function
plot_empirical_quantile(sorted_frequencies)
# Plot the empirical CDF
plot_empirical_cdf(sorted_frequencies)
Για δώσε ενδεικτικά κάποια νούμερα, τι έδωσε;
Νταξει είχαμε πρόοδο, από τις μπαρούφες ότι ο τύπος του είναι ο μόνος σωστός μαθηματικά έχει κάνει backtracking στο ότι θεωρητικά δεν είναι σωστός αλλά εμπειρικά βγάζει ψιλοσωστό αποτέλεσμα αν κάνουμε σωστό cherry picking τα νούμερα 
) αλλά όχι την j 
