Ανίκητος έγραψε: 07 Φεβ 2025, 08:00
nik_killthemall έγραψε: 07 Φεβ 2025, 00:19
Ανίκητος έγραψε: 06 Φεβ 2025, 23:55Τη δική μου γνώμη την εξέφρασα μόλις προηγουμένως και μου είναι
αδιάφορο αν οι παίκτες είναι ανεξάρτητοι, ή εξαρτημένοι, συνεννοούνται, ή αν καθένας παίκτης παίζει παραπάνω ίδιες στήλες γιατί μπορεί (ο @pussycat το έκανε για πλάκα) ή για να κοροϊδέψει τον προπατζή του.
Δεν ασχολούμαι με το τι κάνουν οι παίκτες, πέρα από το τι στήλες υποβάλλουν σαν σύνολο.
Συμφωνω οτι η διατυπωση μου δεν ηταν και η καθαροτερη, απο κει και περα ομως αυτο που λες εδω δεν ισχυει !
Ο τυπος του μπακαλη εχει για ΜΑΘΗΜΑΤΙΚΗ ΠΡΟΥΠΟΘΕΣΗ αυτο που εδω λες οτι σου ειναι αδιαφορο : Την ανεξαρτησια των στηλων ! Αν οι στηλες δεν ειναι ανεξαρτητες τοτε απαγορευεται η πιθανοτητα τομης ενδεχομενων να σπασει σε
γινομενα πιθανοτητων ωστε να δωσει τον τυπο του μπακαλη. Εδω θα σε καλεσω εγω να
φρεσκαρεις τις πιθανοτητες και τι ισχυει με τα ανεξαρτητα ενδεχομενα.
Ωραία, έκανα το φρεσκάρισμά μου.
Παίρνω λοιπόν δυο διαφορετικές παιγμένες στήλες i και j και θεωρώ δυο ενδεχόμενα:
έστω A
i το ενδεχόμενο η στήλη i να μην κληρωθεί νικήτρια, έχει πιθανότητα 1-(1/ν)
και A
j το ενδεχόμενο η στήλη j να μην κληρωθεί νικήτρια, έχει πιθανότητα 1-(1/ν)
Όταν συντρέχουν και τα δύο ενδεχόμενα, τότε κάποια τρίτη στήλη, παιγμένη ή όχι, έχει κληρωθεί.
Αν συμβεί η j να μην είναι νικήτρια, πώς επηρεάζει το ενδεχόμενο η i να μην είναι ούτε αυτή νικήτρια;
Εξήγησέ μου πώς γίνεται η δεσμευμένη P(A
i|A
j) ≠ P(A
i), που είναι ο άλλος τύπος για την ανεξαρτησία.
Μεγαλώνει, ή μικραίνει η πιθανότητα του ενδεχομένου A
i, όταν συμβεί το A
j;
Ή δείξε μου ποια είναι η πιθανότητα της τομής των ενδεχομένων A
i ∩ A
j, αν δεν είναι (1-1/ν)^2.
(Μου θυμίζει την ίδια αντίληψη που παρασύρεται πολύς κόσμος, ότι έχει πολύ καιρό να κληρωθεί το τάδε νούμερο τζόκερ, άρα θα πρέπει να κληρωθεί σύντομα, προκειμένου να "εξοφλήσει" την μεροληψία των προηγούμενων κληρώσεων, να αποκαταστήσει την αμεροληψία. Αλλά η ανεξαρτησία των κληρώσεων σημαίνει το αντίθετο.)
Στο απεδειξα αυτο που ζητας οταν ν=6 (μια ζαρια) και παιχτες = 3 ! Τοτε η πιθανοτητα ειναι (1-c1/ν)*(1-c2/ν)*(1-c3/ν) οπου c1,c2,c3 οι διαφορετικες στηλες που θα εχει παιξει ο καθε παιχτης και αυτο επειδη οι στηλες δεν θα ειναι ανεξαρτητες αλλα θα ειναι οι παιχτες !
Μπορεις να πας εδω στο σποιλερ που σου εχω δειξει καμια 30αρια φορες εως τωρα την αποδειξη και να μου αποδειξεις το λαθος ! Και μην μου πεις για παιδικα πειραματα κλπ υπαρχει κατι που λεγεται και αναδρομικη αποδειξη. (αποδειξη για ν=1, για ν=ν, για ν=ν+1), δεν χρειαζεται να παιδευεσαι με τα εκ συνδυασμων ντε και καλα.
Ορισμοι :
U = ενωση (ή)
/ = δεσμευμενη πιθανοτητα
^ = τομη (και)
Ενδεχομενο να μην πετυχει κανενας το αποτελεσμα της ζαριας = Α
Ενδεχομενο να ειναι και τα 4 πονταρισματα διαφορετικα = Β
Ενδεχομενο να ειναι ιδια μονο 2 πονταρισματα = Γ = 3 διαφορετικα πονταρισματα
Ενδεχομενο να ειναι ιδια μονο 3 πονταρισματα = Δ = 2 διαφορετικα πονταρισματα
Λύση :
Απο τη στιγμη που ο ενας απο τους τρεις πχωρουμιτες θα παιξει 2 διαφορετικα πονταρισματα και οχι ΙΔΙΑ, δεν προκειται να εμφανιστουν ΠΟΤΕ 4 ιδια πονταρισματα, οποτε ολοι οι δυνατοι συνδυασμοι των 4 πονταρισματων ΔΕΝ θα ειναι 6*6*6*6, αλλα θα ειναι (6*5)*6*6 !
Τα Β,Γ,Δ και παλι ειναι ξενα μεταξυ τους και η ενωση τους εχει πιθανοτητα 1 ! Και συγκεκριμενα :
P(Β) = (6*5*4*3)/(6*5*6*6) = 12/36 = 33.33%
P(Γ) = (6*5 *4 + 2*6*4*5 +2*6*4*5) /(6*5*6*6) = 20/36 = 55,55%
P(Δ) = (6*5*2 + 6*5*2)/(6*5*6*6) = 4/36 = 11,11%
Δεσμευμενες πιθανοτητες :
P(A/Β) = 2/6
P(A/Γ) = 3/6
P(A/Δ) = 4/6
Θεωρημα Ολικης πιθανοτητας
P(A) = P( A^(ΒUΓUΔ) ) = P( (A^B)U(A^Γ)U(A^Δ) ) = P(A^B) + P(A^Γ) + P(A^Δ) ) = P(A/B)*P(B) + P(A/Γ)*P(Γ) + P(A/Δ)*P(Δ) =
(2/6)*(12/36) + (3/6)*(20/36) + (4/6)*(4/36) => P(A) = 100 / 216 = (5/6) * (5/6)*(4/6) = (1-1/6)*(1-1/6)*(1-2/6).
Το μονο πραγμα που προσαπτεις σε αυτην την αποδειξη ειναι το γιατι εξαιρω τις διπλες στηλες οχι διαφορετικων παιχτων αυτες δεν τις εξαιρω καθολου τις υπολογιζω, αλλα τις διπλες στηλες του ιδιου παιχτη !
Και το προσαπτεις αυτο γιατι προφανως θεωρεις πως στη πραγματικοτητα του τζοκερ το πληθος των παιχτων που θα συμπληρωνουν δελτια με ιδιες στηλες ειναι χιλιαδες και εκατομμυρια

που εγω παω παρατυπα και τις βγαζω εκτος δειγματικου χωρου !
Ενω εγω θεωρω πως αυτα τα δελτια θα ειναι μηδεν και γιαυτο τις εξαιρω απο τον δειγματικο χωρο !
Γιαυτο λεω οτι δεν διαφωνουμε στα μαθηματικα αλλα διαφωνουμε για το τι συμβαινει στη πραγματικοτητα των παικτων που παιζουν τζοκερ !
Οποιος πιστευει οτι οι παιχτες τζοκερ παιζουν εκ δελτια με ιδιες στηλες σε καθε δελτιο τοτε ασφαλως και οφειλει να διαφωνησει με την εξαιρεση διπλων στηλων του ιδιου παιχτη που κανω στην αποδειξη !
Σε αυτο που γραφεις εδω εσυ θεωρεις οτι καθε παιχτης παιζει ακριβως μια στηλη, γιαυτο ισχυει αυτο που γραφεις ΑΝ οντως στο τζοκερ καθε παιχτης επαιζε μονο μια στηλη.
Στο πραγματικο τζοκερ ομως οι παικτες παιζουν πανω απο μια στηλη ! Το να πεις οτι δεν με ενδιαφερουν οι παιχτες και ποσες στηλες παιζει καθε παιχτης ειναι σαν να λες πως μια πληροφορια για το πειραμα που σου ειναι ορατη να την κανεις επιτηδες αορατη !
Ειναι σα να σου δινει καποιος κατευθειαν τις διακριτες στηλες και να λες οχι δεν θελω να τις ξερω για να βγει ο τυπος υπολογισμου που επιθυμω.
Ανίκητος έγραψε: 07 Φεβ 2025, 08:00
nik_killthemall έγραψε: 07 Φεβ 2025, 00:19
Παμε παρακατω, η P' της διωνυμικης εκφραζει την πιθανοτητα που υπαρχει σε 24 εκ επαναληψεις του πειραματος σου να προκυψουν
s επιτυχιες !
Εσυ τωρα πρεπει να εξηγησεις ΓΙΑΤΙ οι s επιτυχιες στο πειραμα σου σημαινουν s διακριτες στηλες μεσα στις παιγμενες ! Επιτυχια στο πειραμα σου ετσι οπως εσυ την ορισες, ειναι μια στηλη απο τις 24 εκ να μην βρισκεται μεσα στις παιγμενες στηλες αφου θα εχει πολλαπλοτητα ki = 0 !
Πως αυτο ειναι ισοδυναμο με τις διακριτες στηλες των m ? Πρεπει να το εξηγησεις γιατι δεν ειναι αυτονοητο.
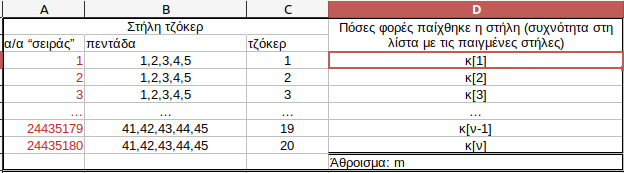
Οι m στήλες μέσα στη λίστα με παιγμένες, μπορεί να επαναλαμβάνονται, αλλά εξακολουθεί να υπάρχει το ενδεχόμενο κάποια στήλη από τις ν=24435180 να έχει παραλειφθεί από τις παιγμένες. Και δεν εννοώ να έχει παραλειφθεί μόνο μία στήλη από τις ν, αλλά μία ή περισσότερες από τις ν. Αυτό περιορίζει τον αριθμό των διακριτών στηλών μέσα στις παιγμένες από ν σε s. Οι παιγμένες είναι m και μέσα τους υπάρχουν s διακριτές, όπου s≤v.
Έβαλα k
i=0 αν έχει παραλειφθεί η στήλη i από τις v. Μια υπο-ομάδα των k
i (i=1..ν) θα έχει πλήθος s, άθροισμα m, ενώ τα υπόλοιπα θα είναι μηδενικά. Ε
το κόλπο ο κόπος είναι πώς υπεισέρχονται (v-s) μηδενικά σε v προσθετέους του αθροίσματος m.
Ε δεν ξέρω τι άλλο να πω 10 χρονών ανίψι έχω θα το καταλάβει.
Οχι δεν θα το καταλαβει ετσι οπως το λες !
Τοσην ωρα σου ζηταω να μου υποδειξεις ποια ειναι η εξισωση που σου προσφερει η διωνυμικη και σε αυτην την εξισωση που ειναι ο αγνωστος διακριτες στηλες που θα υπολογισεις και ποιοι ειναι οι γνωστοι και δεν μου δειχνεις ουτε την εξισωση ουτε ουτε τον αγνωστο !
Παμε παλι η διωνυμικη σου δινει μια εξισωση P' = F(ν,s,m)
Σε αυτην την εξισωση ποιοι ειναι οι γνωστοι και ποιοι οι αγνωστοι που υπολογιζεις ! Για να βρω το s σε αυτην την εξισωση ΠΡΕΠΕΙ να γνωριζω το P' το οποιο για να το υπολογισεις πρεπει να ξερεις το s που εσυ ψαχνεις !
Αν καποιος σου δωσει το P', ηδη γνωριζεις το ν και το m, αρα με καποια επαναληπτικη διαδικασια λυνεις την εξισωση και υπολογιζεις το s το οποιο θα ειναι οι φορες που στις ν = 24 εκ δοκιμες
ΔΕΝ ηρθαν στηλες που βρισκονται στις παιγμενες με πιθανοτητα P' ! Αυτο που μολις εγραψα σημαινει πως το s ΔΕΝ ΕΙΝΑΙ οι διακριτες στηλες των παιγμενων ετσι οπως πηγες και ορισες την επιτυχια στο πειραμα σου ! Το s ειναι οι διακριτες στηλες αυτων που ΔΕΝ παιχτηκαν και γιαυτο δεν εμφανιστηκαν στις παιγμενες εχοντας ki=0 ! Αρα για να βρεις τις διακριτες στηλες των παιγμενων m πρεπει να αφαιρεσεις απτα 24 εκ το s !
Τοσην ωρα προσπαθω να σου δειξω πως
ετσι οπως πηγες και ορισες την επιτυχια στο πειραμα σου το s ΔΕΝ ΕΙΝΑΙ οι διακριτες στηλες των παιγμενων, κι ο αντιλογος ειναι οτι μικρα παιδια θα σε καταλαβαιναν ... αμα δε βγαλεις και το τουπε δεν μπορεις ...
Με λιγα λογια επρεπε να ορισεις σαν επιτυχια στο πειραμα σου το αναποδο δηλ. ki>0 !!! αλλάζοντας αντιστοιχα και τον τυπο p που ετσι κι αλλιως τον μεταφερεις χωρις να τον καταλαβαινεις γιατι ειναι ετσι ! ΤΟΤΕ πραγματι το s ΘΑ ΗΤΑΝ οι διακριτες στηλες των παιγμενων !
Και πολυ ωραια τα διορθωνεις τα παραπανω, αλλα
το P' απο που στο διαολο το βρισκεις ωστε στην P' = F(ν,s,m), ο μοναδικος αγνωστος να ειναι το s ?
Μην μου πεις απο την διωνυμικη γιατι η διωνυμικη ειναι η εξισωση που λυνεις !
Για να εχεις την απαιτηση να καταλαβει κατι ακομα και παιδακι, ΠΡΕΠΕΙ ΝΑ ΤΟ ΕΧΕΙΣ πρωτα καταλαβει εσυ ! Το εχεις ?