ST48410 έγραψε: 02 Μαρ 2021, 10:34
nrg έγραψε: 02 Μαρ 2021, 10:31
ST48410 έγραψε: 01 Μαρ 2021, 12:23
Δεν συμφωνώ. Υπάρχουν περιθώρια βελτίωσης αλλά δεν τα θεωρώ σκουπίδια. Στο διαδίκτυο πλέον συνοδεύονται από αναλυτικό υλικό τόσο για τον εκπαιδευτικό όσο και ψηφιακό υλικό για το μαθητή. Παράλληλα υπάρχουν και τετράδια εργασιών και το φωτόδεντρο με επιπλέον υλικό που μπορεί να χρησιμοποιηθεί συμπληρωματικά.
Δεν ξέρω τι έχεις υπόψη σου και πως θα ήταν ένα καλό βιβλίο πχ δημοτικού. Τι θα είχε παραπάνω και τι θα αφαιρούσες από τα δικά μας. Δεν έχω άποψη από βιβλία ίδιων τάξεων άλλων χωρών. Τι παραπάνω έχουν; Θα ήθελα να ακούσω και γνώμες άλλων.
Δεν νοείται σοβαρό βιβλίο που να μην έχει και απαιτητικά λυμένα παραδείγματα. Και με βάση αυτά να υπάρχουν αντίστοιχες και πολλές ασκήσεις. Εκεί είναι που αποδεσμεύεσαι από την ποιότητα του καθηγητή και παράλληλα τα παιδιά μπορεί να κάνουν δουλειά και εξάσκηση για το σπίτι.
Στα σχολικά βιβλία, τα παραδείγματα είναι της πλάκας και κακογραμμένα, όσο δεν πάει. Οι δε ασκήσεις για λύση κατά συντριπτικό ποσοστό, δεν έχουν σχέση με τα λυμένα παραδείγματα. Θυμάμαι και το λυσάρι που όταν το διάβαζα, ξεχνούσα και αυτά που ήξερα...
Για αυτό και οι σοβαροί καθηγητές στα σχολεία (ναι υπάρχουν και τέτοιοι) δίνουν φωτοτυπίες. Γιατί τα σχολικά βιβλία είναι σκουπίδια.
Και αν δεν κάνω λάθος οι φωτοτυπίες απαγορεύονται...
Κρυφό σχολειό στον 21 αιώνα...
Θέλω να ακούσω και άλλες γνώμες πάνω σε αυτό. Μιλάς για βιβλία κάποιας συγκεκριμένης χρονιάς ή γενικά;
Κατά τη γνώμη μου δεν είναι πρόβλημα τα βιβλία.
Πολύ πρόσφατα παραδείγματα, στα οποία χωρίς την βοήθεια του μπαμπά θα είχαμε πρόβλημα.
Οδηγία β: "...και έπειτα τοποθετούμε την υποδιαστολή στην σωστή θέση."
Μόνο που δεν γράφει πουθενά πώς γίνεται η "τοποθέτηση" της υποδιαστολής. Το αφήνουν στην φαντασία των παιδιών...
Και ένα παιδάκι του δημοτικού πρέπει να καταλάβει από το παράδειγμα δίπλα ότι:
β1. μετράμε όλα τα δεκαδικά ψηφία που έχουν οι αριθμοί που πολλαπλασιάζουμε και
β2. στο αποτέλεσμα μετακινούμε την υποδιαστολή προς τα αριστερά τόσες θέσεις, όσα και τα ψηφία που μετρήσαμε.
Υπόψιν. Το βιβλίο δεν γράφει πουθενά ότι:
"
Ακόμα και οι ακέραιοι αριθμοί έχουν στο τελευταίο τους ψηφίο υποδιαστολή, που για λόγους ευκολίας δεν την γράφουμε."
Παράδειγμα: 12,0 = 12 και 12,00 = 12 αλλά και 12,000... = 12
Για να καταλάβει το παιδί που στα κομμάτια είναι η ριμάδα η υποδιαστολή σε έναν αριθμό που ΔΕΝ βλέπει την υποδιαστολή.
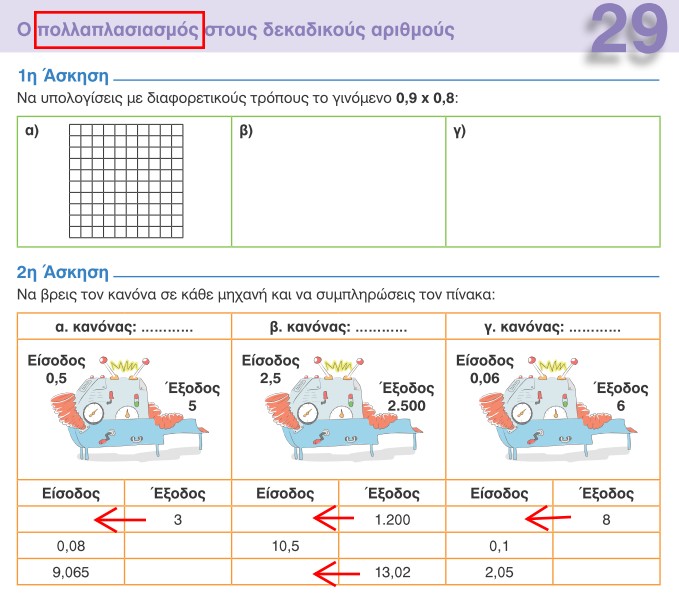
Άσκηση στο ίδιο μάθημα.
Πάνω γράφει πολλαπλασιασμός, αλλά στην άσκηση εκεί που έχω βάλει τα βέλη πρέπει να κάνεις διαίρεση...
Να γελάς και να κλαίς...
Αλλάζουμε τάξη...
Η παρακάτω εικόνα του βιβλίου (εκείνη με τα 3 δοχεία), τυπωμένη έχει διαστάσεις 3,5 x 2 cm (έλεος... το βιβλίο έχει άπειρα κενά, αλλά ας κάνουμε την εικόνα μικροσκοπική... γυμνάζουμε και τα μάτια...)
Από εκεί ο μαθητής πρέπει να καταλάβει
με το μάτι, ότι τα δοχεία έχουν το ίδιο εμβαδόν βάσης. Αλλά η βάση των δοχείων ΔΕΝ φαίνεται σε αυτό το σχήμα-σκουπίδι.
Αν είναι να λύνουμε ασκήσεις με το μάτι, τότε στην γεωμετρία γιατί μας έλεγαν να αποδείξουμε ότι τα τρίγωνα είναι ίσα;... Αφού ίσα φαίνονται...
Αυτά τα πράγματα είναι απαράδεκτα και τα αλίευσα έτσι για πλάκα από τα βιβλία, γιατί τα παιδιά ζήτησαν διευκρινήσεις.
Βιβλία σκουπίδια, χωρίς υπερβολή.
( Διαμαντοπούλου) , για 3 μήνες δεν είχαμε! σχολικά βιβλία και δουλεύαμε με φωτοτυπίες. 