Τρίγωνα

[wooded glade]

Δίδονται έξη τυχαία σημεία στο επίπεδο μη συνευθειακά ανά τρία.
Ενώνωντας τις κορυφές των έξη σημείων σχηματίζονται 20 τρίγωνα.
Να αποδείξετε ότι από αυτά τα τρίγωνα υπάρχουν δύο στα οποία η μικρότερη πλευρά του ενός ισούται προς την μεγαλύτερη πλευρά του άλλου.

[mao mao]

Ζόρικο. Δεν νομίζω να λύνεται στο χέρι.

[ST48410]

λειτουργεί για κάθε διάταξη των έξι σημείων; Αν έχεις εξάγωνο τα εσωτερικά μεγάλα τρίγωνα είναι ισόπλευρα και δεν έχεις πλέον μεγάλη πλευρά.

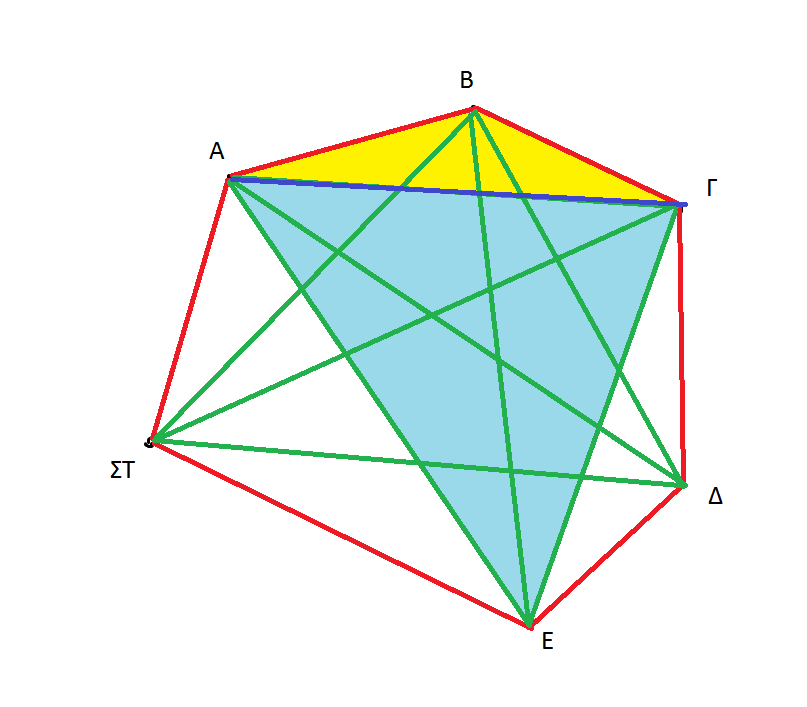
Αλλιώς πχ η ΑΓ

[wooded glade]

Για να βοηθήσω είναι περισσότερο πρόβλημα συνδυαστικής παρά γεωμετρίας.

[nick]

Φαινεται πρόβλημα για μαθηματικές ολυμπιαδες.

[mao mao]

λειτουργεί για κάθε διάταξη των έξι σημείων; Αν έχεις εξάγωνο τα εσωτερικά μεγάλα τρίγωνα είναι ισόπλευρα και δεν έχεις πλέον μεγάλη πλευρά.

Αλλιώς πχ η ΑΓ

και η ΒΔ. Το θέμα είναι όμως πως αποδεικνύεις οτι αυτό ισχύει για οποιαδήποτε 6 σημεία του χώρου, μη συνευθειακά ανα τρία.

[ST48410]

λειτουργεί για κάθε διάταξη των έξι σημείων; Αν έχεις εξάγωνο τα εσωτερικά μεγάλα τρίγωνα είναι ισόπλευρα και δεν έχεις πλέον μεγάλη πλευρά.

Αλλιώς πχ η ΑΓ

και η ΒΔ. Το θέμα είναι όμως πως αποδεικνύεις οτι αυτό ισχύει για οποιαδήποτε 6 σημεία του χώρου, μη συνευθειακά ανα τρία.

ναι. Οι μαθηματικές μου γνώσεις δε φτάνουν μέχρι εκεί. Αυτό που διαισθάνομαι είναι ότι τρία σημεία που είναι κάπως μακρύτερα από ένα τέταρτο (που μάλλον θα υπάρχει τέτοια τετράδα αναγκαστικά) θα μπορούν να δώσουν τέτοιο ζευγάρι τριγώνων.

[nick]

Πρεπει να παιζει το οτι ειναι τουλαχιστον 6 σημεια (με λιγοτερα μαλλον δεν ισχύει).
Αθροισμα γωνιών =180*(6-2)=720 μοίρες, αρα καποια γωνια ειναι >120 (π.χ. Α).
Η πλευρα απενταντι απο Α ειναι η μεγαλυτερη για το τριγωνο Α-Β-ΣΤ, αλλα πρεπει καποια απο τις ΒΓΣΤ ή ΒΔΣΤ ή ΒΕΣΤ να ειναι <45 ...

[ST48410]

μήπως μπορεί να αποδειχθεί ότι για 6 σημεία (που ανά τρία είναι μη συνευθειακά) θα υπάρχει πάντα μία τετράδα που το ένα θα είναι μακρύτερα από το τρίγωνο που ορίζουν τα άλλα τρία (και άρα η γωνία <45);

[Ζενίθεδρος]

λειτουργεί για κάθε διάταξη των έξι σημείων; Αν έχεις εξάγωνο τα εσωτερικά μεγάλα τρίγωνα είναι ισόπλευρα και δεν έχεις πλέον μεγάλη πλευρά.

Αλλιώς πχ η ΑΓ

και η ΒΔ. Το θέμα είναι όμως πως αποδεικνύεις οτι αυτό ισχύει για οποιαδήποτε 6 σημεία του χώρου, μη συνευθειακά ανα τρία.

Του επιπέδου, οχι του χώρου. Επίσης, δε λέει για κυρτό 6γωνο, αλλα για έξι σημεία του επιπέδου. Το εξάγωνο μπορει να ειναι και μη κυρτό.

[NoMoreLice]

Για να βοηθήσω είναι περισσότερο πρόβλημα συνδυαστικής παρά γεωμετρίας.

Γκουγκλάροντας είδα πως λύνεται με τη βοήθεια ενός θεωρήματος από γράφους. Συνδυαστική πώς; Πέρα από το να δεις ότι έχεις 20 τρίγωνα, 15 ευθ. τμήματα και ότι το κάθε ευθ. τμήμα συμμετέχει σε 4 τρίγωνα. Αλλά μετά δεν βγαίνει πουθενά έτσι.

[mao mao]

Πέρα από το να δεις ότι έχεις 20 τρίγωνα, 15 ευθ. τμήματα και ότι το κάθε ευθ. τμήμα συμμετέχει σε 4 τρίγωνα. Αλλά μετά δεν βγαίνει πουθενά έτσι.

και εγώ έτσι προσπάθησα να το λύσω, αλλά έφτασα σε αδιέξοδο.