Άσκηση πιθανοτήτων για δυνατούς λύτες

[wooded glade]

Δύο αθλητές, ο Κεντέρης και η Θάνου, τρέχουν τα 100 μέτρα σε χρόνους Τ1 ο ένας και Τ2 ο άλλος.
Η μέση απόκλιση του καθενός είναι σ1 και σ2 αντίστοιχα.
Ποιά σχέση πρέπει να υφίσταται μεταξύ Τ1, σ1 και Τ2, σ2 ώστε ο Κεντέρης να έχει μεγαλύτερη πιθανότητα να έρθει πρώτος ;
Αν σ1 = σ2, τότε προφανώς η σχέση είναι Τ1 < Τ2, αλλά δεν είναι ίσα τα σ.

[stavmanr]

Εδώ, δυστυχώς, απαιτούνται δεδομένα χημικής τεχνολογίας που δεν διαθέτουμε, ούτε εμείς ούτε σύγχρονοι διεθνείς οργανισμοί.

[Χουργιατς]

Η μέση απόκλιση

[mao mao]

Δύο αθλητές, ο Κεντέρης και η Θάνου, τρέχουν τα 100 μέτρα σε χρόνους Τ1 ο ένας και Τ2 ο άλλος.
Η μέση απόκλιση του καθενός είναι σ1 και σ2 αντίστοιχα.
Ποιά σχέση πρέπει να υφίσταται μεταξύ Τ1, σ1 και Τ2, σ2 ώστε ο Κεντέρης να έχει μεγαλύτερη πιθανότητα να έρθει πρώτος ;
Αν σ1 = σ2, τότε προφανώς η σχέση είναι Τ1 < Τ2, αλλά δεν είναι ίσα τα σ.

μάλλον με ασαφή λογική λύνεται αυτό που είναι σχετική με θεωρία πιθανοτήτων. Δεν είναι για δυνατούς λύτες.

Πρέπει όμως να ξέρουμε την κατανομή της απόκλισης.

[Yochanan]

pΚεντερης ~ N(T1-T2,(σ1^2+σ2^2)^0,5)

[wooded glade]

Δύο αθλητές, ο Κεντέρης και η Θάνου, τρέχουν τα 100 μέτρα σε χρόνους Τ1 ο ένας και Τ2 ο άλλος.
Η μέση απόκλιση του καθενός είναι σ1 και σ2 αντίστοιχα.
Ποιά σχέση πρέπει να υφίσταται μεταξύ Τ1, σ1 και Τ2, σ2 ώστε ο Κεντέρης να έχει μεγαλύτερη πιθανότητα να έρθει πρώτος ;
Αν σ1 = σ2, τότε προφανώς η σχέση είναι Τ1 < Τ2, αλλά δεν είναι ίσα τα σ.

μάλλον με ασαφή λογική λύνεται αυτό που είναι σχετική με θεωρία πιθανοτήτων. Δεν είναι για δυνατούς λύτες.

Πρέπει όμως να ξέρουμε την κατανομή της απόκλισης.

Η κατανομή είναι η κανονική.
Η πιθανότητα πάντως έχει τον εξής τύπο:

P1 = ολοκλήρωμα (f1 x FC2)

όπου f1 η PDF του "1" και FC2 η συμπληρωματική CDF του "2" (complementary error function).
Δεν ξέρω τη συνθήκη.

[mao mao]

Η κατανομή είναι η κανονική.

Εφόσον μιλάμε για κανονικές κατανομές τα πράγματα είναι απλά.
https://imgur.com/a/07TiOXu

Εστω με μπλε οι η κατανομή των χρόνων του Κεντέρη, και με κόκκινο οι χρόνοι της Θάνου. Διαφορετική μέση τιμή και αποκλίσεις.

https://imgur.com/a/Q2EnIg2

Η Θάνου περνάει τον Κεντέρη στο σκιαγραφημένο διάστημα. Ουσιαστικά ψάχνεις την πιθανότητα ο χρόνος του Κεντέρη και της Θάνου να είναι ταυτόχρονα μικρότερος του Χ1 ή ο χρόνους τους να είναι ταυτόχρονα μεγαλύτερος του Χ2

Εφόσον μιλάμε για κανονικές κατανομές με γνωστές μέσες τιμές και τυπικές αποκλίσεις, αυτές οι πιθανότητες βρίσκονται από τυπολόγιο.

[sys3x]

Γουντ, έχεις καβαλήσει άτι; σε αγώνα εννοάω.

[wooded glade]

χχχχχχχχχχχχχχχχχχχχχχχχχχχχχχχχχχχχχχχχχχχ

[wooded glade]

Η κατανομή είναι η κανονική.

Εφόσον μιλάμε για κανονικές κατανομές τα πράγματα είναι απλά.
https://imgur.com/a/07TiOXu

Εστω με μπλε οι η κατανομή των χρόνων του Κεντέρη, και με κόκκινο οι χρόνοι της Θάνου. Διαφορετική μέση τιμή και αποκλίσεις.

https://imgur.com/a/Q2EnIg2

Η Θάνου περνάει τον Κεντέρη στο σκιαγραφημένο διάστημα. Ουσιαστικά ψάχνεις την πιθανότητα ο χρόνος του Κεντέρη και της Θάνου να είναι ταυτόχρονα μικρότερος του Χ1 ή ο χρόνους τους να είναι ταυτόχρονα μεγαλύτερος του Χ2

Εφόσον μιλάμε για κανονικές κατανομές με γνωστές μέσες τιμές και τυπικές αποκλίσεις, αυτές οι πιθανότητες βρίσκονται από τυπολόγιο.

Ναι είναι το σκιαγραφημένο χωρίο.
Εγώ σου δίνω και τον τύπο ο οποίος το ολοκλήρωμα βγαίνει με Simpson's rule πολύ εύκολα για δεδομένα νούμερα.
Αλλά η σχέση λέμε.
Θα μπορούσα ίσως να βάλω Τ1=10, σ1=1 και Τ2, σ2 μεταβλητά και να σχεδιάσω χαρακτηριστικές καμπύλες.

[wooded glade]

Γουντ, έχεις καβαλήσει άτι; σε αγώνα εννοάω.

Μιά φορά είδα στον ύπνο μου.

[wooded glade]

Δύσκολο έργο.
Θέτω Τ1 - Τ2 = Ε και σ2 = k . σ1 και κάνω κάτι νορμαλοποιήσεις και βγαίνει:

P1 = σ1 . ολ/μα { f(x) . Fc ( x/k + E / (k . σ1) ) }

Είναι δηλαδή συνάρτησις τριών παραμέτρων.

[Who is The 4th man]

Η κατανομή είναι η κανονική.

Εφόσον μιλάμε για κανονικές κατανομές τα πράγματα είναι απλά.
https://imgur.com/a/07TiOXu

Εστω με μπλε οι η κατανομή των χρόνων του Κεντέρη, και με κόκκινο οι χρόνοι της Θάνου. Διαφορετική μέση τιμή και αποκλίσεις.

https://imgur.com/a/Q2EnIg2

Η Θάνου περνάει τον Κεντέρη στο σκιαγραφημένο διάστημα. Ουσιαστικά ψάχνεις την πιθανότητα ο χρόνος του Κεντέρη και της Θάνου να είναι ταυτόχρονα μικρότερος του Χ1 ή ο χρόνους τους να είναι ταυτόχρονα μεγαλύτερος του Χ2

Εφόσον μιλάμε για κανονικές κατανομές με γνωστές μέσες τιμές και τυπικές αποκλίσεις, αυτές οι πιθανότητες βρίσκονται από τυπολόγιο.

Ναι είναι το σκιαγραφημένο χωρίο.
Εγώ σου δίνω και τον τύπο ο οποίος το ολοκλήρωμα βγαίνει με Simpson's rule πολύ εύκολα για δεδομένα νούμερα.
Αλλά η σχέση λέμε.
Θα μπορούσα ίσως να βάλω Τ1=10, σ1=1 και Τ2, σ2 μεταβλητά και να σχεδιάσω χαρακτηριστικές καμπύλες.

εννοείς τό ολοκλήρωμα τής κανονικής Gauss μέ γενική μορφή;


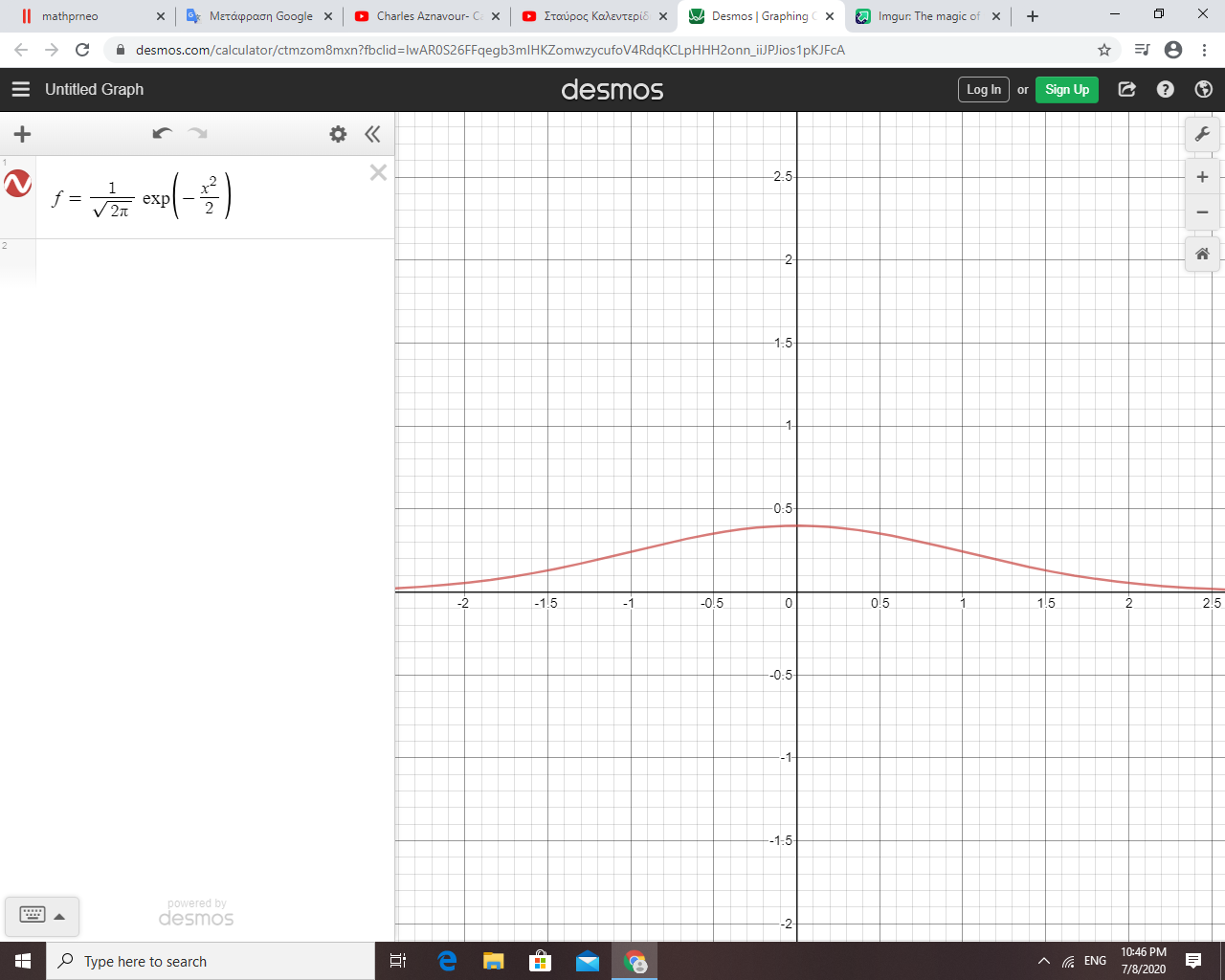
ποιούς συντελεστές έχεις βάλει,ροτάω γιατί τό έχεις θέσει γενικά,
καί βέβαια δεν υπολογίζεται μέ κλασικές μεθόδους αλλά μέ Υπολογιστικά Μαθς

[BlastFromThePast]

Δύο αθλητές, ο Κεντέρης και η Θάνου, τρέχουν τα 100 μέτρα σε χρόνους Τ1 ο ένας και Τ2 ο άλλος.
Η μέση απόκλιση του καθενός είναι σ1 και σ2 αντίστοιχα.
Ποιά σχέση πρέπει να υφίσταται μεταξύ Τ1, σ1 και Τ2, σ2 ώστε ο Κεντέρης να έχει μεγαλύτερη πιθανότητα να έρθει πρώτος ;
Αν σ1 = σ2, τότε προφανώς η σχέση είναι Τ1 < Τ2, αλλά δεν είναι ίσα τα σ.

Τ1 και Τ2 είναι μέσοι όροι; Τότε Τ1<Τ2 αρκεί.

[Στύγιος]

Δύο αθλητές, ο Κεντέρης και η Θάνου, τρέχουν τα 100 μέτρα σε χρόνους Τ1 ο ένας και Τ2 ο άλλος.
Η μέση απόκλιση του καθενός είναι σ1 και σ2 αντίστοιχα.
Ποιά σχέση πρέπει να υφίσταται μεταξύ Τ1, σ1 και Τ2, σ2 ώστε ο Κεντέρης να έχει μεγαλύτερη πιθανότητα να έρθει πρώτος ;
Αν σ1 = σ2, τότε προφανώς η σχέση είναι Τ1 < Τ2, αλλά δεν είναι ίσα τα σ.

Τζέκος κι ο "μαγικός ζωμός" είναι η λύση.