Phorum.com.gr

Ασέβαστος έγραψε: 10 Μαρ 2023, 19:40

Spoiler

εδω η σωστη, κατα τη μαθηματικη εταιρεια, απαντηση. αυτη εδωσε ο γιος.

γω εδωσα ... την αλλη

λοιπον; να τους βγαλουμε σκιντζηδες κι αυτους η να τσακωθουμε λιγο πρωτα;

Αν θεωρήσουμε τους δρόμους σαν γραμμές, χωρίς πλάτος, το σωστό είναι το 1.
Δεν γνωρίζουμε ακριβείς διαστάσεις (μήκος, πλάτος) για να κάνουνε υπολογισμούς.

Α ναι, οι εσωτερικοι δρομοι ειναι λιγο πιο μικροι.

Ασέβαστος έγραψε: 10 Μαρ 2023, 19:47

Dwarven Blacksmith έγραψε: 10 Μαρ 2023, 19:41 Ίσα είναι εκτός αν μετρήσεις τις γωνίες. Αλλά οι μαθηματικοί δεν είναι μηχανικοί, γι αυτούς είναι απλά ευθύγραμμα τμήματα.
Άρα σίγουρα το 1.

αν ηθελαν να βγαλουν ασκηση με ευθυγραμμα τμηματα, επρεπε να σχεδιασουν ευθυγραμμα τμηματα, και τοτε θα ηταν το 1.

αλλα αφου σχεδιασαν δρομο, με πλατος > 0, δεν ειναι.

Απευθύνονται σε παιδιά και ήθελαν κάτι πιο πρακτικό. Αλλά πάλι ισχύει το "έστω σημειακές κότες με σημειακά αυγά". Το πλάτος δεν αναφέρεται, άρα δεν μπορούν να γίνουν πράξεις με αυτό, άρα το έχουν κάνει assume away, άρα ευθύγραμμα τμήματα.

Σέλευκας έγραψε: 10 Μαρ 2023, 19:42 βεβαια τωρα που το ξανασκέφτομαι οι τέσσερις γωνίες που υπολοίπονται είναι αλληλοκάλυψη των γραμμών στο πράσινο. Αν προσθέσουμε την αλληλοκάλυψη που είναι πάλι τεσσερις γωνίες ιδιο βγαίνει

αν "σηκωσουμε" τους πρασινους δρομους, και τους ακουμπησουμε πανω στους γκρι, θα τους καλυψουν εντελως η θα μεινει ορατο λιγο γκρι;

vatraxos έγραψε: 10 Μαρ 2023, 19:45 Επίσης, βλέπω κι άλλο ένα ζήτημα. Θα προσμετρηθεί στο μήκος κάθε επί μέρους εσωτερικού δρόμου και το κοινό τμήμα τους;

Αν τα προσμετρήσεις, γιατί να μην προσμετρήσεις και τα κοινά τμήματα με τον περιφερειακό; Επειδή είναι με διαφορετικό χρώμα;

η διαφορα ειναι

Περιφερειακος = Αθροισμα εσωτερικων +4χ(2χ(Πλατος Περιφερειακου/2)²)

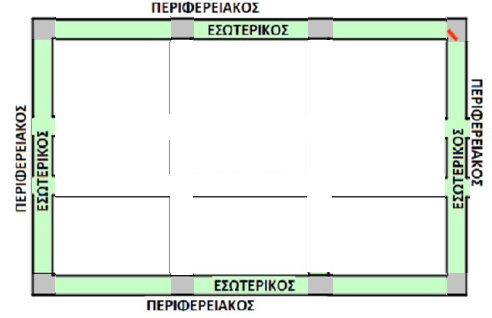
βγαλαμε του εσωτερικους και τους βαλαμε πανω στον περιφερειακο για να χαμπεριασεται τι γινεται

βλεπετε το κοκκινο στην γωνια;

Nandros έγραψε: 10 Μαρ 2023, 19:48

Ασέβαστος έγραψε: 10 Μαρ 2023, 19:40

Spoiler

εδω η σωστη, κατα τη μαθηματικη εταιρεια, απαντηση. αυτη εδωσε ο γιος.

γω εδωσα ... την αλλη

λοιπον; να τους βγαλουμε σκιντζηδες κι αυτους η να τσακωθουμε λιγο πρωτα;

Αν θεωρήσουμε τους δρόμους σαν γραμμές, χωρίς πλάτος, το σωστό είναι το 1.
Δεν γνωρίζουμε ακριβείς διαστάσεις (μήκος, πλάτος) για να κάνουνε υπολογισμούς.

ναι, αλλα αν ηθελε κατι τετοιο η ασκηση, ας σχεδιαζε γραμμες. εφοσον σχεδιασε δρομους, με καποιο πλατος, πρεπει να παρει απαντηση που να αφορα δρομους.

Ασέβαστος έγραψε: 10 Μαρ 2023, 19:54

Nandros έγραψε: 10 Μαρ 2023, 19:48

Ασέβαστος έγραψε: 10 Μαρ 2023, 19:40

Spoiler

εδω η σωστη, κατα τη μαθηματικη εταιρεια, απαντηση. αυτη εδωσε ο γιος.

γω εδωσα ... την αλλη

λοιπον; να τους βγαλουμε σκιντζηδες κι αυτους η να τσακωθουμε λιγο πρωτα;

Αν θεωρήσουμε τους δρόμους σαν γραμμές, χωρίς πλάτος, το σωστό είναι το 1.
Δεν γνωρίζουμε ακριβείς διαστάσεις (μήκος, πλάτος) για να κάνουνε υπολογισμούς.

ναι, αλλα αν ηθελε κατι τετοιο η ασκηση, ας σχεδιαζε γραμμες. εφοσον σχεδιασε δρομους, με καποιο πλατος, πρεπει να παρει απαντηση που να αφορα δρομους.

Σε αυτή την περίπτωση διαλέγω το 5.

Dwarven Blacksmith έγραψε: 10 Μαρ 2023, 19:50

Ασέβαστος έγραψε: 10 Μαρ 2023, 19:47

Dwarven Blacksmith έγραψε: 10 Μαρ 2023, 19:41 Ίσα είναι εκτός αν μετρήσεις τις γωνίες. Αλλά οι μαθηματικοί δεν είναι μηχανικοί, γι αυτούς είναι απλά ευθύγραμμα τμήματα.
Άρα σίγουρα το 1.

αν ηθελαν να βγαλουν ασκηση με ευθυγραμμα τμηματα, επρεπε να σχεδιασουν ευθυγραμμα τμηματα, και τοτε θα ηταν το 1.

αλλα αφου σχεδιασαν δρομο, με πλατος > 0, δεν ειναι.

Απευθύνονται σε παιδιά και ήθελαν κάτι πιο πρακτικό. Αλλά πάλι ισχύει το "έστω σημειακές κότες με σημειακά αυγά". Το πλάτος δεν αναφέρεται, άρα δεν μπορούν να γίνουν πράξεις με αυτό, άρα το έχουν κάνει assume away, άρα ευθύγραμμα τμήματα.

Δεν χρειαζεται να ξερεις το πλατος του περιφερειακου... Δες την απο πανω αναρτηση... ειναι απλουστατο... Εκανα επαφη με τον Πυθαγορα μεσω Medium...

vagabondo έγραψε: 10 Μαρ 2023, 19:52

vatraxos έγραψε: 10 Μαρ 2023, 19:45 Επίσης, βλέπω κι άλλο ένα ζήτημα. Θα προσμετρηθεί στο μήκος κάθε επί μέρους εσωτερικού δρόμου και το κοινό τμήμα τους;

Αν τα προσμετρήσεις, γιατί να μην προσμετρήσεις και τα κοινά τμήματα με τον περιφερειακό; Επειδή είναι με διαφορετικό χρώμα;

Δεν ξέρω, ρωτάω. Ο χρωματισμός σε συνδυασμό με το πλάτος του δρόμου κάνει την απάντηση περίπλοκη. Και όταν στις απαντήσεις μπαίνουν διαφορές τύπου 3/4 και 2/3, μου φαίνονται ήδη άκυρες ως ενδεχόμενα. Μένει να είναι ίδιο το μήκος ή να μην είναι σωστή καμία απάντηση, που όμως πρέπει να τεκμηριωθεί σε σχέση με τις δύο που ανέφερα. Που δε γίνεται γιατί λογικά δεν τους λένε πάρτε χάρακα να μετρήσετε πλάτος δρόμων.

taxalata xalasa έγραψε: 10 Μαρ 2023, 19:56

Dwarven Blacksmith έγραψε: 10 Μαρ 2023, 19:50

Ασέβαστος έγραψε: 10 Μαρ 2023, 19:47

αν ηθελαν να βγαλουν ασκηση με ευθυγραμμα τμηματα, επρεπε να σχεδιασουν ευθυγραμμα τμηματα, και τοτε θα ηταν το 1.

αλλα αφου σχεδιασαν δρομο, με πλατος > 0, δεν ειναι.

Απευθύνονται σε παιδιά και ήθελαν κάτι πιο πρακτικό. Αλλά πάλι ισχύει το "έστω σημειακές κότες με σημειακά αυγά". Το πλάτος δεν αναφέρεται, άρα δεν μπορούν να γίνουν πράξεις με αυτό, άρα το έχουν κάνει assume away, άρα ευθύγραμμα τμήματα.

Δεν χρειαζεται να ξερεις το πλατος του περιφερειακου... Δες την απο πανω αναρτηση... ειναι απλουστατο...

Την είδα

taxalata xalasa έγραψε: 10 Μαρ 2023, 19:52 η διαφορα ειναι

Περιφερειακος = Αθροισμα εσωτερικων +4χ(2χ(Πλατος Περιφερειακου/2)²)

βγαλαμε του εσωτερικους και τους βαλαμε πανω στον περιφερειακο για να χαμπεριασεται τι γινεται

βλεπετε το κοκκινο στην γωνια;

Κοινώς ΔΕΝ μπορείς να βγάλεις αποτέλεσμα και λες απλά "δεν είναι ίσα, είναι κάτι άλλο".

Dwarven Blacksmith έγραψε: 10 Μαρ 2023, 19:50

Ασέβαστος έγραψε: 10 Μαρ 2023, 19:47

Dwarven Blacksmith έγραψε: 10 Μαρ 2023, 19:41 Ίσα είναι εκτός αν μετρήσεις τις γωνίες. Αλλά οι μαθηματικοί δεν είναι μηχανικοί, γι αυτούς είναι απλά ευθύγραμμα τμήματα.
Άρα σίγουρα το 1.

αν ηθελαν να βγαλουν ασκηση με ευθυγραμμα τμηματα, επρεπε να σχεδιασουν ευθυγραμμα τμηματα, και τοτε θα ηταν το 1.

αλλα αφου σχεδιασαν δρομο, με πλατος > 0, δεν ειναι.

Απευθύνονται σε παιδιά και ήθελαν κάτι πιο πρακτικό. Αλλά πάλι ισχύει το "έστω σημειακές κότες με σημειακά αυγά". Το πλάτος δεν αναφέρεται, άρα δεν μπορούν να γίνουν πράξεις με αυτό, άρα το έχουν κάνει assume away, άρα ευθύγραμμα τμήματα.

τετοιες μαλακιες δεν επιτρεπονται οταν δηλωνεις "μαθηματικη εταιρεια" μπορουσαν μια χαρα να πουν ευθυγραμμα τμηματα. η εστω, αν ηθελαν να το κανουν ευπεπτο για παιδια, ας ελεγαν δρομοι, αλλα να σχεδιαζαν ευθυγραμμα τμηματα.

η τελοσπαντων, να μην εβαζαν καν μια ασκηση που μπορει να ερμηνευτει με 2 τροπους.

Dwarven Blacksmith έγραψε: 10 Μαρ 2023, 19:57

taxalata xalasa έγραψε: 10 Μαρ 2023, 19:56

Dwarven Blacksmith έγραψε: 10 Μαρ 2023, 19:50
Απευθύνονται σε παιδιά και ήθελαν κάτι πιο πρακτικό. Αλλά πάλι ισχύει το "έστω σημειακές κότες με σημειακά αυγά". Το πλάτος δεν αναφέρεται, άρα δεν μπορούν να γίνουν πράξεις με αυτό, άρα το έχουν κάνει assume away, άρα ευθύγραμμα τμήματα.

Δεν χρειαζεται να ξερεις το πλατος του περιφερειακου... Δες την απο πανω αναρτηση... ειναι απλουστατο...

Την είδα

taxalata xalasa έγραψε: 10 Μαρ 2023, 19:52 η διαφορα ειναι

Περιφερειακος = Αθροισμα εσωτερικων +4χ(2χ(Πλατος Περιφερειακου/2)²)

βγαλαμε του εσωτερικους και τους βαλαμε πανω στον περιφερειακο για να χαμπεριασεται τι γινεται

βλεπετε το κοκκινο στην γωνια;

Κοινώς ΔΕΝ μπορείς να βγάλεις αποτέλεσμα και λες απλά "δεν είναι ίσα, είναι κάτι άλλο".

το πλατος του περιφερειακου ειναι Χ... βαλε Χ και εχεις την εξισωση. Παντως ισα δεν ειναι... Το 5 ειναι η σωστη απαντηση.

Ασέβαστος έγραψε: 10 Μαρ 2023, 19:58

Dwarven Blacksmith έγραψε: 10 Μαρ 2023, 19:50

Ασέβαστος έγραψε: 10 Μαρ 2023, 19:47

αν ηθελαν να βγαλουν ασκηση με ευθυγραμμα τμηματα, επρεπε να σχεδιασουν ευθυγραμμα τμηματα, και τοτε θα ηταν το 1.

αλλα αφου σχεδιασαν δρομο, με πλατος > 0, δεν ειναι.

Απευθύνονται σε παιδιά και ήθελαν κάτι πιο πρακτικό. Αλλά πάλι ισχύει το "έστω σημειακές κότες με σημειακά αυγά". Το πλάτος δεν αναφέρεται, άρα δεν μπορούν να γίνουν πράξεις με αυτό, άρα το έχουν κάνει assume away, άρα ευθύγραμμα τμήματα.

τετοιες μαλακιες δεν επιτρεπονται οταν δηλωνεις "μαθηματικη εταιρεια" μπορουσαν μια χαρα να πουν ευθυγραμμα τμηματα. η εστω, αν ηθελαν να το κανουν ευπεπτο για παιδια, ας ελεγαν δρομοι, αλλα να σχεδιαζαν ευθυγραμμα τμηματα.

η τελοσπαντων, να μην εβαζαν καν μια ασκηση που μπορει να ερμηνευτει με 2 τροπους.

ελα τωρα που εγινες και αυστηρος με το τι δηλωνουν!... Ο αλλος ειναι selfie junkie παραμυθας Mr. Bean και δηλωνει άριστος επιτελάρχης...

Ασέβαστος έγραψε: 10 Μαρ 2023, 19:47

Dwarven Blacksmith έγραψε: 10 Μαρ 2023, 19:41 Ίσα είναι εκτός αν μετρήσεις τις γωνίες. Αλλά οι μαθηματικοί δεν είναι μηχανικοί, γι αυτούς είναι απλά ευθύγραμμα τμήματα.
Άρα σίγουρα το 1.

αν ηθελαν να βγαλουν ασκηση με ευθυγραμμα τμηματα, επρεπε να σχεδιασουν ευθυγραμμα τμηματα, και τοτε θα ηταν το 1.

αλλα αφου σχεδιασαν δρομο, με πλατος > 0, δεν ειναι.

Μα πως σχεδιάζεται ένας δρόμος χωρίς πλάτος; Απλώς στη συγκεκριμένη φάση, έχει σημασία το πλάτος του περιφερειακού ενώ των εσωτερικών, όχι. Και αν δεν ξέρεις το πλάτος, σαφώς και δεν παίζουν άλλες απαντήσεις εκτός από την 1 και 5.

Για να το θέσω διαφορετικά, σκεφθείτε ένα συγκρότημα κατοικιών ή ένα ορθογώνιο κτίσμα (όπως στα λευκά κουτιά της εικόνας) χωρίς περιβάλλοντα χώρο. Θα είναι το σύνολο της περιμέτρου του ίσο με το μήκος των δρόμων που το περιβάλλουν;