Άσκηση πιθανοτήτων για δυνατούς λύτες

[Yochanan]

Δύο αθλητές, ο Κεντέρης και η Θάνου, τρέχουν τα 100 μέτρα σε χρόνους Τ1 ο ένας και Τ2 ο άλλος.
Η μέση απόκλιση του καθενός είναι σ1 και σ2 αντίστοιχα.
Ποιά σχέση πρέπει να υφίσταται μεταξύ Τ1, σ1 και Τ2, σ2 ώστε ο Κεντέρης να έχει μεγαλύτερη πιθανότητα να έρθει πρώτος ;
Αν σ1 = σ2, τότε προφανώς η σχέση είναι Τ1 < Τ2, αλλά δεν είναι ίσα τα σ.

Τ1 και Τ2 είναι μέσοι όροι; Τότε Τ1<Τ2 αρκεί.

συμφωνω κι αυτο εγραψα και πιο πανω. η κατανομη της διαφορας τους (αν μιλαμε για standard normal - δλδ συμμετρικη) ειναι Ν(Τ1-Τ2,(σ1^2+σ2^2)^0,5) νομιζω. Αυτο θα εχει παντα median T1 - T2 και το 50% + θα εξαρταται μονο απο αυτη τη διαφορα

[wooded glade]

Δύο αθλητές, ο Κεντέρης και η Θάνου, τρέχουν τα 100 μέτρα σε χρόνους Τ1 ο ένας και Τ2 ο άλλος.
Η μέση απόκλιση του καθενός είναι σ1 και σ2 αντίστοιχα.
Ποιά σχέση πρέπει να υφίσταται μεταξύ Τ1, σ1 και Τ2, σ2 ώστε ο Κεντέρης να έχει μεγαλύτερη πιθανότητα να έρθει πρώτος ;
Αν σ1 = σ2, τότε προφανώς η σχέση είναι Τ1 < Τ2, αλλά δεν είναι ίσα τα σ.

Τ1 και Τ2 είναι μέσοι όροι; Τότε Τ1<Τ2 αρκεί.

Μπορεί.

[wooded glade]

Να ο τύπος του ολοκληρώματος εν πάσει περιπτώσει:

https://www.untruth.org/~josh/math/normal-min.pdf

[wooded glade]

Το ολοκλήρωμα του Hill του προηγουμένου ποστ δεν είναι παρά ένα απλό corollary του Bayes.

Στο πρόβλημα τώρα κατ' αρχάς θα χρησιμοποιήσω την ψευδοκατανομή της μορφής f(x) = 1 / ( 1 + x^2 ) και όχι την κανονική που είναι η μορφή exp(-x^2).
Αυτό για να γίνει το ολοκλήρωμα πιό εύκολο αλλά δεν πειράζει γιατί είναι συμμετρικές και οι δύο.

Έχουμε λοιπόν:

f(t) = C / ( 1 + ((t – T) / σ)^2)
όπου Τ ο μέσος όρος και σ η απόκλιση.
Η σταθερά C της νορμαλοποίησης είναι: C = 1 / (π . σ ).

Η συνάρτηση Fc(t) (το συμπλήρωμα της CDF) είναι:

Fc(t) = 0.5 – atn((t - T) / σ) / π

Η πιθανότητα του (T1, σ1) να βγει πρώτος από τον (Τ2, σ2) είναι τώρα σύμφωνα με τον
τύπο του Hill ίση προς:

P = ολοκλήρωμα { f1 . F2c } = ολοκλήρωμα { (1/(π . σ1)) . ( 0.5 – atn((t - T2) / σ2) / π ) / ( 1 + ((t – T1) / σ1)^2) }

ως προς t από -∞ έως +∞

Θέτω (t – T1) / σ1 = u και γίνεται αυτό:

P = ολοκλήρωμα { (1 / π) . ( 0.5 – atn((σ1/σ2) . u + (T1 - T2) / σ2) / π) / ( 1 + u^2) }

ως προς u από -∞ έως +∞.

Αυτό τώρα το υπολογίζω με composite Simpson’s rule.

Βάζω αρχικά Τ1 = 10, σ1 = 0.50, Τ2 = 10, σ2 = 0.50.
Πρέπει P = 0.5 και θέλω να δω πόση ακρίβεια χρειάζεται ο Simpson’s rule.
Δεν είναι και τόσο απλό. Ίσως θέλει κάποια περαιτέρω διερεύνηση, ως προς
να γίνει μία truncation της κατανομής, να μην πηγαίνει από -∞ ως +∞.
Αλλά εν πάσει περιπτώσει αν βάλω 500,000 subintervals και η έκταση
της κατανομής να είναι -10000 ως +10000 βγαίνει P = .49997, για την
περίπτωση αυτή (που ξέρουμε ότι P = 0.5).
Πετάχτηκα τώρα σε αρνητικά νούμερα για τους χρόνους στα 100 μέτρα
που δεν υπάρχουν !

Δεν προχωράω στις περιπτώσεις που μας ενδιαφέρουν.
Θα το ξανακάνω με truncated distributions.

[wooded glade]

Βάζω λοιπόν

f(t) = C / ( 1 + ((t – T) / σ)^2)

με την κατανομή να εκτείνεται από Τ - Ν . σ έως T + Ν . σ, όπου Ν ~ 4.

Βγαίνει τώρα normalization constant C = 1 / (2 . σ . atn(N)).

και Fc(t) = 0.5 - atn((t - Τ) / σ) / (2 . σ . atn(N)) δια |t - T| <= N . σ, Fc(t) = 1 διά t - T < -4 . N . σ, Fc(t) = 0 δια t - T > 4 . N . σ.

Προχωράω όπως προηγουμένως και βρίσκω με 200 subintervals στον Simpson:

Για (10,.5) και (10,.5) P1 = P2 = 0.5 με ακρίβεια δισεκατομμυριοστών.

Για (10,0.5) και (10.2, 0.7) βγαίνει P1 = 55.8%

Δοκιμάζω διάφορες τιμές, πάντα ο "καλός" έχει μεγαλύτερη πιθανότητα, ανεξαρτήτου μέσων αποκλίσεων.
Άρα κύριοι η μπάλα λέει ότι η συνθήκη είναι T1 < T2. Μάλιστα.

[Yochanan]

Δύο αθλητές, ο Κεντέρης και η Θάνου, τρέχουν τα 100 μέτρα σε χρόνους Τ1 ο ένας και Τ2 ο άλλος.
Η μέση απόκλιση του καθενός είναι σ1 και σ2 αντίστοιχα.
Ποιά σχέση πρέπει να υφίσταται μεταξύ Τ1, σ1 και Τ2, σ2 ώστε ο Κεντέρης να έχει μεγαλύτερη πιθανότητα να έρθει πρώτος ;
Αν σ1 = σ2, τότε προφανώς η σχέση είναι Τ1 < Τ2, αλλά δεν είναι ίσα τα σ.

Τ1 και Τ2 είναι μέσοι όροι; Τότε Τ1<Τ2 αρκεί.

συμφωνω κι αυτο εγραψα και πιο πανω. η κατανομη της διαφορας τους (αν μιλαμε για standard normal - δλδ συμμετρικη) ειναι Ν(Τ1-Τ2,(σ1^2+σ2^2)^0,5) νομιζω. Αυτο θα εχει παντα median T1 - T2 και το 50% + θα εξαρταται μονο απο αυτη τη διαφορα

Σορε, κι ο τυπας αυτο λεει για Ν=2 απλως ειναι γιωτομπαλλο και θελει να παρει ολοκληρωμα εκει που μπορει, ξερω γω, να κανει μια αφαιρεση να δει αν ειναι μεγαλυτερο του 0 ή όχι.

[mao mao]

Μάλιστα, εφόσον όπως γράφουν και τα παιδιά παραπάνω η διαφορά δύο κανονικών κατανομών είναι επίσης κανονική με μέση τιμή Τ1-Τ2 problem solved

[mao mao]

[img]https://i.postimg.cc/SNxtWprg/New- ... .png[/img]

πανεύκολα δλδ γνωρίζοντας τα Τ1, Τ2 , σ1 ,σ2 μπορούμε να υπολογίζουμε από τους πίνακες ακριβώς την πιθανότητα ο Κεντέρης να περάσει τη Θάνου ή το αντίστροφο.

[wooded glade]

Έχει δίκιο ο Yochanan με την παρατήρηση του, αλλά ο υπολογισμός γίνεται από το ολοκλήρωμα. Ποιοί πίνακες ;
Αλλά δεν είναι δύσκολο. Χρόνο μηδέν θέλει για να υπολογιστεί.
Μου έκανε εντύπωση που δεν βγαίνει καλά αν δεν δημιουργήσω την truncated distribution. Έβαλα όριο το 4 . σ αλλά χωρίς αυστηρό κριτήριο.
Το mathematica code που λέει ο άλλος δεν το καταλαβαίνω.

Αν είναι 3 ή 4 ή n οι τρέχτες ισχύει και πάλι το κριτήριο Τ1 <= Τ2 <= ... <= Τn για την διάταξη των πιθανοτήτων ;

[Yochanan]

[img]https://i.postimg.cc/SNxtWprg/New- ... .png[/img]

πανεύκολα δλδ γνωρίζοντας τα Τ1, Τ2 , σ1 ,σ2 μπορούμε να υπολογίζουμε από τους πίνακες ακριβώς την πιθανότητα ο Κεντέρης να περάσει τη Θάνου ή το αντίστροφο.

Μα δεν χρειάζεται να ξέρεις το σ1,σ2 αυτο ειναι το θεμα, ουτε καν το τ1 τ2 μονο αν τ1>τ2

[wooded glade]

[img]https://i.postimg.cc/SNxtWprg/New- ... .png[/img]

πανεύκολα δλδ γνωρίζοντας τα Τ1, Τ2 , σ1 ,σ2 μπορούμε να υπολογίζουμε από τους πίνακες ακριβώς την πιθανότητα ο Κεντέρης να περάσει τη Θάνου ή το αντίστροφο.

Μα δεν χρειάζεται να ξέρεις το σ1,σ2 αυτο ειναι το θεμα, ουτε καν το τ1 τ2 μονο αν τ1>τ2

Ναι, δεν πρόσεξα ότι το t1 - t2 είναι normal distribution του sqr(σ1^2 + σ2^2), οπόταν φαίνεται απ' ευθείας.
Αλλά για να κάνεις υπολογισμούς μόνο με το ολοκλήρωμα του Hill γίνονται και μου δημιουργεί πρόσθετες απορίες.
Μία είναι πως ακριβώς ορίζουμε την truncated distribution για να κάνουμε τον προσεγγιστικό υπολογισμό ;
Η άλλη είναι επεκτείνεται το κριτήριο Τ1 < Τ2 και σε μεγαλύτερο πλήθος αθλητών ;

[mao mao]

[img]https://i.postimg.cc/SNxtWprg/New- ... .png[/img]

πανεύκολα δλδ γνωρίζοντας τα Τ1, Τ2 , σ1 ,σ2 μπορούμε να υπολογίζουμε από τους πίνακες ακριβώς την πιθανότητα ο Κεντέρης να περάσει τη Θάνου ή το αντίστροφο.

Μα δεν χρειάζεται να ξέρεις το σ1,σ2 αυτο ειναι το θεμα, ουτε καν το τ1 τ2 μονο αν τ1>τ2

Nαι συμφωνώ με αυτό. Το αρχικό ερώτημα του Wooded δεν χρειάζεται καμία επιπλέον ανάλυση, αρκεί Τ1>Τ2

Αυτό που θέλω να πω είναι οτι αν γνωρίζεις και τα σ1.σ2 μπορείς να υπολογίσεις ακριβώς την πιθανότητα η Θάνου να περάσει τον Κεντέρη. Γνωρίζουμε οτι είναι <50% εφόσον Τ1>Τ2 αλλά μπορούμε να υπολογίσουμε πχ οτι είναι 15%.

[Yochanan]

πανεύκολα δλδ γνωρίζοντας τα Τ1, Τ2 , σ1 ,σ2 μπορούμε να υπολογίζουμε από τους πίνακες ακριβώς την πιθανότητα ο Κεντέρης να περάσει τη Θάνου ή το αντίστροφο.

Μα δεν χρειάζεται να ξέρεις το σ1,σ2 αυτο ειναι το θεμα, ουτε καν το τ1 τ2 μονο αν τ1>τ2

Nαι συμφωνώ με αυτό. Το αρχικό ερώτημα του Wooded δεν χρειάζεται καμία επιπλέον ανάλυση, αρκεί Τ1>Τ2

Αυτό που θέλω να πω είναι οτι αν γνωρίζεις και τα σ1.σ2 μπορείς να υπολογίσεις ακριβώς την πιθανότητα η Θάνου να περάσει τον Κεντέρη. Γνωρίζουμε οτι είναι <50% εφόσον Τ1>Τ2 αλλά μπορούμε να υπολογίσουμε πχ οτι είναι 15%.

κατάλαβα, ωραίος

[mao mao]

Έχει δίκιο ο Yochanan με την παρατήρηση του, αλλά ο υπολογισμός γίνεται από το ολοκλήρωμα. Ποιοί πίνακες ;
Αλλά δεν είναι δύσκολο. Χρόνο μηδέν θέλει για να υπολογιστεί.
Μου έκανε εντύπωση που δεν βγαίνει καλά αν δεν δημιουργήσω την truncated distribution. Έβαλα όριο το 4 . σ αλλά χωρίς αυστηρό κριτήριο.
Το mathematica code που λέει ο άλλος δεν το καταλαβαίνω.

Αν είναι 3 ή 4 ή n οι τρέχτες ισχύει και πάλι το κριτήριο Τ1 <= Τ2 <= ... <= Τn για την διάταξη των πιθανοτήτων ;

Δεν ξέρω τι είναι το truncated distribution, θα σου κάνω ένα υπολογισμό με παράδειγμα σχετικά με το αρχικό σου ποστ, ίσως σε βοηθήσει


'Εστω ο Κεντέρης τρέχει τα 100m μέσο όρο Τ1 =10.5 sec και τυπική απόκλιση σ1 = 0.5 sec

Η Θάνου τρέχει τα 100μ μέσο όρο T2 =10.8 sec με τυπική απόκλιση σ2 = 0.6 sec.

Όπως είπαμε και παραπάνω η T2-T1 είναι μια κανονική κατανομή έστω T3 =0.3 με τυπική απόκλιση s3= sqrt( s1^2 + s2^) = 0.78 sec.

Η πιθανότητα η Θάνου να περάσει τον Κεντέρη ισούται με την πιθανότητα η κατανομή Τ3 να είναι μικρότερη του 0.

Αυτή η πιθανότητα βρίσκεται εύκολα αν χρησιμοποιήσουμε τον πίνακα με τις τιμές Ζ της standard normal distrubution. ( μ =0 , σ =1 )

Ζ = (Χ - Τ3 / σ3 ) . Εμείς ενδιαφερόμαστε για την πιθανότητα η Τ3<0, οπότε θέτουμε Χ=0 . Επομένως Ζ = -0.3 / 0.78 = > z = -0.384.

Πηγαίνουμε στους πίνακες του Ζ.


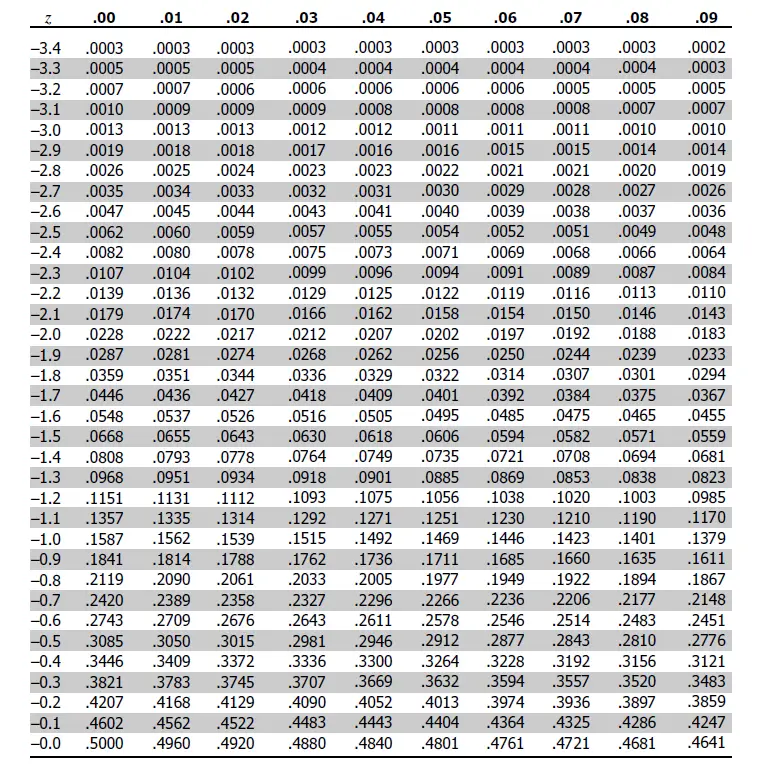
Από τον πίνακα, για τιμές Ζ περίπου ίσο με -0.38, βλέπουμε οτι η πιθανότητα είναι περίπου 35%. ( τιμή πίνακα 0.3520)

Όποιος διαφωνεί το συζητάμε.

[wooded glade]

Έχει δίκιο ο Yochanan με την παρατήρηση του, αλλά ο υπολογισμός γίνεται από το ολοκλήρωμα. Ποιοί πίνακες ;
Αλλά δεν είναι δύσκολο. Χρόνο μηδέν θέλει για να υπολογιστεί.
Μου έκανε εντύπωση που δεν βγαίνει καλά αν δεν δημιουργήσω την truncated distribution. Έβαλα όριο το 4 . σ αλλά χωρίς αυστηρό κριτήριο.
Το mathematica code που λέει ο άλλος δεν το καταλαβαίνω.

Αν είναι 3 ή 4 ή n οι τρέχτες ισχύει και πάλι το κριτήριο Τ1 <= Τ2 <= ... <= Τn για την διάταξη των πιθανοτήτων ;

Δεν ξέρω τι είναι το truncated distribution, θα σου κάνω ένα υπολογισμό με παράδειγμα σχετικά με το αρχικό σου ποστ, ίσως σε βοηθήσει


'Εστω ο Κεντέρης τρέχει τα 100m μέσο όρο Τ1 =10.5 sec και τυπική απόκλιση σ1 = 0.5 sec

Η Θάνου τρέχει τα 100μ μέσο όρο T2 =10.8 sec με τυπική απόκλιση σ2 = 0.6 sec.

Όπως είπαμε και παραπάνω η T2-T1 είναι μια κανονική κατανομή έστω T3 =0.3 με τυπική απόκλιση s3= sqrt( s1^2 + s2^) = 0.78 sec.

Η πιθανότητα η Θάνου να περάσει τον Κεντέρη ισούται με την πιθανότητα η κατανομή Τ3 να είναι μικρότερη του 0.

Αυτή η πιθανότητα βρίσκεται εύκολα αν χρησιμοποιήσουμε τον πίνακα με τις τιμές Ζ της standard normal distrubution. ( μ =0 , σ =1 )

Ζ = (Χ - Τ3 / σ3 ) . Εμείς ενδιαφερόμαστε για την πιθανότητα η Τ3<0, οπότε θέτουμε Χ=0 . Επομένως Ζ = -0.3 / 0.78 = > z = -0.384.

Πηγαίνουμε στους πίνακες του Ζ.


Από τον πίνακα, για τιμές Ζ περίπου ίσο με -0.38, βλέπουμε οτι η πιθανότητα είναι περίπου 35%. ( τιμή πίνακα 0.3520)

Όποιος διαφωνεί το συζητάμε.

Βγαίνει κι έτσι επειδή είναι απλό με δύο τρέχτες και καταλήγει σε μιά μονοδιάστατη pdf.
Αλλά εγώ θέλω και με 3-4-5 ... 20.
Γι αυτό πάμε Hill.
Θα μπορούσα εγώ να κάνω τον υπολογισμό με βάση την κανονική κατανομή, που βγαίνει με κάτι πολυώνυμα 9ου βαθμού οι προσέγγιση της CDF αλλά δε με νοιάζει και πήγα με την πιό απλή f(x) = 1 / ( 1 + x^2 ). Έβαλα λοιπόν όριο συν πλην 4 . σ. Και με την erf πάλι συν πλην 4 . σ θα έβαζα, αλλά πόσο πρέπει να βάλω κανονικά ;