Antares έγραψε: 17 Μαρ 2021, 14:41
stavmanr έγραψε: 13 Μαρ 2021, 22:35
Antares έγραψε: 11 Μαρ 2021, 19:25
Είναι το ιδεατό, αν πλησιάσουμε περισσότερο σε αυτά τα σχήματα που έχεις παραθέσει θα ανακαλύψουμε και άλλες διαστάσεις, ότι δεν είναι ακριβώς κύκλοι κ.ο.κ.
Ξέρεις ποιο είναι το λάθος σε αυτές τις διατυπώσεις που διαβάζουμε από τον Χελετζέ;
Ότι τα γεωμετρικά σχήματα αφορούν
γεωμετρικούς τόπους σημείων που έχουν συγκεκριμένες ιδιότητες.
Αυτό επίσης σημαίνει ότι ως "ιδιότητα" δεν χρειάζεται να θέσουμε το εκάστοτε μόριο ή άτομο, αλλά πχ. το μέσο όρο απόστασης κλπ.
Ο κύκλος είναι μία
λογική συνέπεια της ιδιότητας των σημείων. Γι' αυτό και τον χρησιμοποιούμε για κάθε ορισμό του σημείου, σε κάθε επιστήμη κι όπως κι αν το εννοήσουμε.
Επίσης, το αντικείμενο στο οποίο αναφέρεται ο Χελετζές ονομάζεται "τέλειος κύκλος". Είναι σα να μιλάμε στη Φυσική για "μηχανή εσωτερικής καύσης με απόδοση 100%", που αποτελεί μεν φυσικό όρο, αλλά δεν έχει καμία πρακτική εφαρμογή.
Κάθε γεγονός στη φύση αποτελεί γεωμετρικό τόπο σημείων με συγκεκριμένη ιδιότητα.
Δεν γνωρίζω πολλά από φιλοσοφία της επιστήμης, καταλαβαίνω την άποψή σου, η εξέλιξη της φυσικής και των μαθηματικών είναι πια αμφίδρομη διαδικασία. Τα μαθηματικά δημιουργούν φυσική αλλά και η φυσική μαθηματικά.
Μη σε βάζει κάτω.
Κι εγώ ρακοσυλλέκτης είμαι.
Η Φυσική δεν παράγει Μαθηματικά.
Οι σύγχρονοι φυσικοί, ειδικά αστροφυσικοί, είναι ήδη μαθηματικοί κατά βάση.
Διάβασα και τα προηγούμενα ποστ σχετικά με τους αλληλοεπικαλυπτόμενους κύκλους και την επιφάνεια που δημιουργούν. Ενδιαφέροντα.
Το φως σε συμπαντικές αποστάσεις δεν διαδίδεται ευθεία νομίζω αλλά σε γεωδαισιακές καμπύλες λόγω της καμπύλωσης του χωρόχρονου. Σε μικρές κλίμακες μοιάζουν με ευθείες.
Πρόσεξε τώρα αυτά που έγραφα ακόμα πιο πριν:
η ευθεία (όπως και κάθε απεικόνιση) δεν είναι ένα σχήμα, μία γραμμή, μία ζωγραφιά.
Είναι ένας ορισμός, μία περιγραφή ή και ένα αξίωμα. Αυτό σημαίνει ότι η ευθεία δεν είναι ένα και μοναδικό πράγμα. Είναι "
ένα αποτέλεσμα της εφαρμογής του αξιώματος/ορισμού/πρότασης σε κάθε πλαίσιο αναφοράς".
Αυτό σημαίνει με τη σειρά του ότι η ευθεία σε καμπύλα επίπεδα (μη ευκλείδεια) είναι απλά ...καμπύλη ως προς το ευκλείδειο επίπεδο με το οποίο τη συγκρίνουμε. Σε απλή γλώσσα "ακολουθεί το ανάγλυφο του επιπέδου αναφοράς". Αν έχεις ένα κοίλο επίπεδο, τότε η εκάστοτε
ευθεία του επιπέδου θα είναι ...κοίλη. Η ίδια ευθεία, εξεταζόμενη υπό άλλο επίπεδο αναφοράς, είναι μη κοίλη. Μπορεί να είναι και κυρτή.
Έτσι, όταν παρατηρούμε το φως να προσπερνά έναν αστέρα, θεωρούμε αρχικά ότι κάμπτεται η ευθεία της διάδοσής του. Προσπαθήσαμε να αιτιολογήσουμε γιατί συμβαίνει αυτό και δεν μας έβγαινε.
Ήρθε η Σχετικότητα να μας πείσει ότι απλά κάμπτεται το επίπεδο αναφοράς (χωροχρονικό) ενώ
η διάδοση του φωτός συνεχίζει να γίνεται ευθύγραμμα επάνω στο κοίλο πλέον χωροχρονικό "σεντόνι". Πρόκειται για αμιγώς γεωμετρικό φαινόμενο, που αφορά επιπεδομετρία μη ομαλών (μη ευκλείδειων) επιπέδων. Έτσι, γνωρίζουμε ότι σε καμπυλωμένο μέρος του χωροχρόνου, το φως ακουλουθεί γεωδαισιακές τροχιές, που είναι ...καμπυλωμένες ευθείες.
Ιδιαίτερο ενδιαφέρον έχει να σκεφτείς τι θα ίσχυε αν ο χωροχρόνος, δηλαδή το επίπεδο αναφοράς, ήταν η επιφάνεια μίας σφαίρας.
Κι εδώ έρχονται οι θεωρήσεις του big bang και τα γνωστά παραδείγμα του σύμπαντος που φουσκώνει, αλλά σπάνια κανείς αντιλαμβάνεται ότι το "φούσκωμα" δεν είναι τριδιάστατο, δεν αφορά όγκο. Αυτό που αντιλαμβάνεσαι ως "όγκος" του σύμπαντος, δηλαδή χώρος, είναι απλά μία επιφάνεια σφαίρας.
Οι φυσικοί μας όμως δεν σταματούν εκεί. Αρχίζουν να αντιλαμβάνονται ότι οι γεωμετρίες μας δεν έχουν αρχή και τέλος. Αν μπεις στη διαδικασία να ορίζεις επίπεδα αναφοράς, μπαίνεις σε ένα νέο σύμπαν!
Προσπάθησε να αντιληφθείς πώς είναι να ζεις σε ένα σύμπαν που ο χωροχρόνος του έχει την εξής γεωμετρία (τοπολογία):
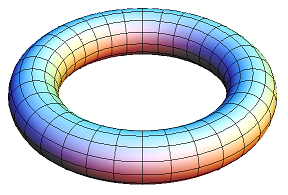
Κάθε γραμμή, στην επιπεδομετρία του συγκεκριμένου σχήματος, είναι και μία ευθεία!
Δεν είναι όμορφα τα μαθηματικά μας;


