Καλώς ήρθατε στο Phorum.com.gr Είμαστε εδώ πολλά ενεργά μέλη της διαδικτυακής κοινότητας του Phorum.gr που έκλεισε. Σας περιμένουμε όλους!
https://dev.phorum.com.gr/
Δεν θα το αποφευγαμε, αλλα το πείραμα θα γινοταν σε επομενο μαθημα για να δειξει την εννοια των συνθετων κλασματων, δηλ. κλασματα που ειναι ισοδυναμα.enaon έγραψε: 10 Δεκ 2022, 12:33ωραία παντως που το λές αυτό, το είπε και ο εθερέαλ εχθές, οτι δεν πρέπει να εμφανίσουν το 24 να μην τα μπερδέψουν.
αν ηταν πείραμα, ειχαν 3 ψευτικες σοκολάτες, τις σπαγανε όγδοα και τα μοιράζανε, πως θα αποφευγαμε να δουνε το 24;
Το κάνουν λίγο πιο απλά γιατί το ίδιο το κλάσμα είναι από μόνο του οι πληροφορίες που παραλείπονται. Ο αριθμητής υποδεικνύει πόσες σοκολάτες είχες και ο παρονομαστής σε πόσα κομμάτια τις χώρισες.Bill Hicks έγραψε: 10 Δεκ 2022, 12:20η 3η πρόταση έπρεπε να λέει:ethereal έγραψε: 10 Δεκ 2022, 03:11Ακόμα μιλάμε για """άσκηση""" και μάλιστα ερήμην δασκάλου;ST48410 έγραψε: 10 Δεκ 2022, 02:59
Εγώ όμως ρώτησα στην πίσω σελίδα πολύ συγκεκριμένα πράγματα. Και οι μαθητές συμβαίνει συχνά να λύνουν ασκήσεις χωρίς την παρουσία και την επεξηγηματική βοήθεια του δασκάλου.
Θα έχει μια διατύπωση η άσκηση και θα περιμένει ο μαθητής να του την εξηγήσει ο δάσκαλος για να προχωρήσει σε λύση; Ε, δεν γίνεται αυτό. Η άσκηση θα πρέπει να είναι διατυπωμένη έτσι που να μην αφήνει απορίες.
Σε αυτό μπορεί να επισημάνει κανείς σε ποια από τις 5 προτάσεις διαφωνεί;
«Επειδή έχουμε τρεις (3) σοκολάτες, τελικά, το κάθε παιδί θα πάρει τρία όγδοα (3/8) σοκολάτας από τις τρεις σοκολάτες.»
Εσύ τι λες να είναι παιδαγωγικό να κάνεις το μυαλό ενός 10χρονου αχταρμά δημιουργώντας πράγματα που δεν υπάρχουν για να λύσεις ένα πρόβλημα του οποίου η λύση είναι υπερβολικά απλή;;enaon έγραψε: 10 Δεκ 2022, 12:59 οπότε γκερ τρείς μέρες που λες το 3/24 ειναι λάθος και δεν καταλαβαινεις που το βρήκε η κασπερ που ειναι μαθηματικός με πλαστό πτυχίο γιατί εκανε πρόσθεση τους παρανομαστές, εννοουσες αντιπαιδαγωγικό;
ωραίος ρε αλήθεια, όταν δεν λες για τον θεούλη τα κειμενά σου για εμένα τουλάχιστον εναι απόλαυση. Με προβληματίζει λίγο γιατι μεχρι να παμε πεμπτη το εχουμε κανει στην πράξη αρκετες φορές αυτό με τις σοκολάτες αν εχαμε ενα αδελφακι κλπ, οπόθε νομιζω καποια παιδια το βλέπουν το 24 ετσι και αλλιως, μου μοιαζει αδύνατον να μην το πει καποιο αν δεν φοβουνται τον δασκαλο, δεν νομιζω οτι αλήθεια ειναι εφικτό να το κρύψουν, αλλα ωραία τα λες.nik_killthemall έγραψε: 10 Δεκ 2022, 13:02 Δεν θα το αποφευγαμε, αλλα το πείραμα θα γινοταν σε επομενο μαθημα για να δειξει την εννοια των συνθετων κλασματων, δηλ. κλασματα που ειναι ισοδυναμα.
Συνεχίζετε να πλακώνεστε για τις σοκολάτες σε ξεχωριστό νήμα;οκ, οποτε τρόλαρες τοσες μερες, το ηξερες οτι μαθηματικά ειναι σωστό αλλα ήθελες απλά να καταλαβουμε οτι ειναι αντιπαιδαγωγικό;Gherschaagk έγραψε: 10 Δεκ 2022, 13:07Εσύ τι λες να είναι παιδαγωγικό να κάνεις το μυαλό ενός 10χρονου αχταρμά δημιουργώντας πράγματα που δεν υπάρχουν για να λύσεις ένα πρόβλημα του οποίου η λύση είναι υπερβολικά απλή;;enaon έγραψε: 10 Δεκ 2022, 12:59 οπότε γκερ τρείς μέρες που λες το 3/24 ειναι λάθος και δεν καταλαβαινεις που το βρήκε η κασπερ που ειναι μαθηματικός με πλαστό πτυχίο γιατί εκανε πρόσθεση τους παρανομαστές, εννοουσες αντιπαιδαγωγικό;
Δλδ πόσο δύσκολο είναι να πεις x αντικείμενα, y άτομα, η λύση είναι x/y των αντικειμένων;
Σταμάτα βρε, λύθηκε η παρεξήγησις.enaon έγραψε: 10 Δεκ 2022, 13:10οκ, οποτε τρόλαρες τοσες μερες, το ηξερες οτι μαθηματικά ειναι σωστό αλλα ήθελες απλά να καταλαβουμε οτι ειναι αντιπαιδαγωγικό;Gherschaagk έγραψε: 10 Δεκ 2022, 13:07Εσύ τι λες να είναι παιδαγωγικό να κάνεις το μυαλό ενός 10χρονου αχταρμά δημιουργώντας πράγματα που δεν υπάρχουν για να λύσεις ένα πρόβλημα του οποίου η λύση είναι υπερβολικά απλή;;enaon έγραψε: 10 Δεκ 2022, 12:59 οπότε γκερ τρείς μέρες που λες το 3/24 ειναι λάθος και δεν καταλαβαινεις που το βρήκε η κασπερ που ειναι μαθηματικός με πλαστό πτυχίο γιατί εκανε πρόσθεση τους παρανομαστές, εννοουσες αντιπαιδαγωγικό;
Δλδ πόσο δύσκολο είναι να πεις x αντικείμενα, y άτομα, η λύση είναι x/y των αντικειμένων;
γιαυτο ελεγες οτ η κασπερ εχει πλαστό πτυχίο, γιατί δεν βλεπει οτι ηταν αντιπαιδαγωγική η σωστή λυση που εδωσε;
Κοίτα αν θες μπορώ κι εγώ να βγάζω λαγούς απ'το κεφάλι μου και να τους χρησιμοποιώ οπότε μου κάνει κέφι για να βγάλω το αποτέλεσμα που με βολεύει και μετά να προσπαθώ να πείσω πως όλο αυτό δεν είναι μια μλκια που φαντάστηκα για να μην ξεβολευτώ και λύσω την άσκηση με τα δεδομένα που μου δίνονται και όχι με αυτά που θα ήθελα εγώ να είχε.enaon έγραψε: 10 Δεκ 2022, 13:10οκ, οποτε τρόλαρες τοσες μερες, το ηξερες οτι μαθηματικά ειναι σωστό αλλα ήθελες απλά να καταλαβουμε οτι ειναι αντιπαιδαγωγικό;Gherschaagk έγραψε: 10 Δεκ 2022, 13:07Εσύ τι λες να είναι παιδαγωγικό να κάνεις το μυαλό ενός 10χρονου αχταρμά δημιουργώντας πράγματα που δεν υπάρχουν για να λύσεις ένα πρόβλημα του οποίου η λύση είναι υπερβολικά απλή;;enaon έγραψε: 10 Δεκ 2022, 12:59 οπότε γκερ τρείς μέρες που λες το 3/24 ειναι λάθος και δεν καταλαβαινεις που το βρήκε η κασπερ που ειναι μαθηματικός με πλαστό πτυχίο γιατί εκανε πρόσθεση τους παρανομαστές, εννοουσες αντιπαιδαγωγικό;
Δλδ πόσο δύσκολο είναι να πεις x αντικείμενα, y άτομα, η λύση είναι x/y των αντικειμένων;
γιαυτο ελεγες οτ η κασπερ εχει πλαστό πτυχίο, γιατί δεν βλεπει οτι ηταν αντιπαιδαγωγική η σωστή λυση που εδωσε;
Το ότι η Κάσπερ βρήκε το σωστό αποτέλεσμα δεν σημαίνει πως έλυσε σωστά την άσκηση. Οπότε στην συγκεκριμένη περίπτωση η μπάλα παίρνει και το σωστό κατά τα άλλα αποτελέσματα.enaon έγραψε: 10 Δεκ 2022, 13:18 γκκερ απλα σου λεω οτι ευχομαστε ολοι να τρολάρεις, αλλα και το τρολάρισμα οταν κανεις προσωπική επίθεση δεν εχει πλακα αν δεν το καταλαβει ο άλλος.
Αυτα που λες μπορουν να καλυφθουν μια χαρα απο διατυπωση της μορφης :Gherschaagk έγραψε: 10 Δεκ 2022, 12:52
Πσιδαγωγικώς, το παιδί μαθαίνει πως όπως μπορεί να χωρίσει ένα πράγμα σε πολλά ίσα μέρη, έτσι μπορεί να χωρίσει πολλά ίδια πράγματα αλλά διαφορετικά μεταξύ τους σε πολλά ίσα μέρη. Επίσης μαθαίνει πως είναι αυθαίρετο να φανταστεί πως αυτά τα πράγματα μπορεί να τα ενώσει με έναν μαγικό τρόπο και να τα κάνει ένα καινούριο πράγμα το οποίο θα χρησιμοποιήσει για να λύσει την άσκηση. Επίσης επειδή κάποια από τα παιδιά όπως θα μοιράζονται τα κομμάτια δεν θα πάρουν κομμάτια από μία σοκολάτα αλλά από 2, ο πληθυντικός διατηρείται γιατί ακόμη και στην εκφώνηση το ζητούμενο ήταν να χωρίσεις 3 σοκολάτες όχι μία. Όταν λες 3/8 της σοκολάτας αφήνεις να εννοηθεί πως είχες μια σοκολάτα την έκοψες σε 8 ίσα μέρη και πήρες τα 3. Μόνο που δεν ήταν μία.
αυτο το εμαθε στην πρωτη δημοτικου.Gherschaagk έγραψε: 10 Δεκ 2022, 12:52
Πσιδαγωγικώς, το παιδί μαθαίνει πως όπως μπορεί να χωρίσει ένα πράγμα σε πολλά ίσα μέρη, έτσι μπορεί να χωρίσει πολλά ίδια πράγματα αλλά διαφορετικά μεταξύ τους σε πολλά ίσα μέρη. Επίσης μαθαίνει πως είναι αυθαίρετο να φανταστεί πως αυτά τα πράγματα μπορεί να τα ενώσει με έναν μαγικό τρόπο και να τα κάνει ένα καινούριο πράγμα το οποίο θα χρησιμοποιήσει για να λύσει την άσκηση. Επίσης επειδή κάποια από τα παιδιά όπως θα μοιράζονται τα κομμάτια δεν θα πάρουν κομμάτια από μία σοκολάτα αλλά από 2, ο πληθυντικός διατηρείται γιατί ακόμη και στην εκφώνηση το ζητούμενο ήταν να χωρίσεις 3 σοκολάτες όχι μία. Όταν λες 3/8 της σοκολάτας αφήνεις να εννοηθεί πως είχες μια σοκολάτα την έκοψες σε 8 ίσα μέρη και πήρες τα 3. Μόνο που δεν ήταν μία.
ε, μα...Ασέβαστος έγραψε: 10 Δεκ 2022, 12:20Spoiler
Bill Hicks έγραψε: 10 Δεκ 2022, 12:07ωραία παραδείγματα ΣΤ. την αριθμητική την αναλύσαμε κι όποιος σκαμπάζει κατάλαβε.ST48410 έγραψε: 10 Δεκ 2022, 01:27Είναι δυνατόν για την ίδια ακριβώς διατύπωση να υπάρχουν 2 λύσεις; Δεν είναι ολοφάνερο πως δημιουργείται πρόβλημα;Spoiler
Αυτό με την γενική είναι απαράδεκτο (κατά την ταπεινή μου γνώμη).
Θα στο εξηγήσω με ένα άλλο παράδειγμα με ελαφρώς διαφορετικά νούμερα. Έστω ότι είχες 2 μήλα και 4 μαθητές. Σύμφωνα με την λογική που χειρίζεται το βιβλίο τον πληθυντικό η απάντηση θα προέκυπτε από την διαίρεση 2 : 4
2/4 μήλων ή με απλοποίηση 1/2 μήλων
Φαντάσου τώρα τον παρακάτω διάλογο:
Γιωργάκης: κυρία, κυρία!
Δασκάλα: λέγε Γιωργάκη
Γ: το 1/2 δεν είναι το μισό
Κ: ναι
Γ: Αν ο πρώτος μαθητής πάρει το μισό των μήλων και ο δεύτερος το άλλο μισό, τότε τι θα μείνει για τους δύο άλλους μαθητές;
Εδώ όπως καταλαβαίνεις θα αναγκαστεί η δασκάλα να εξηγήσει ότι όταν λέει τα 2/4 των μήλων ή το 1/2 των μήλων, εννοεί το 1/2 του ενός μήλου.
Νομίζω ότι είναι ξεκάθαρο πόσο κακή και ασαφής είναι η διατύπωση με τον πληθυντικό.
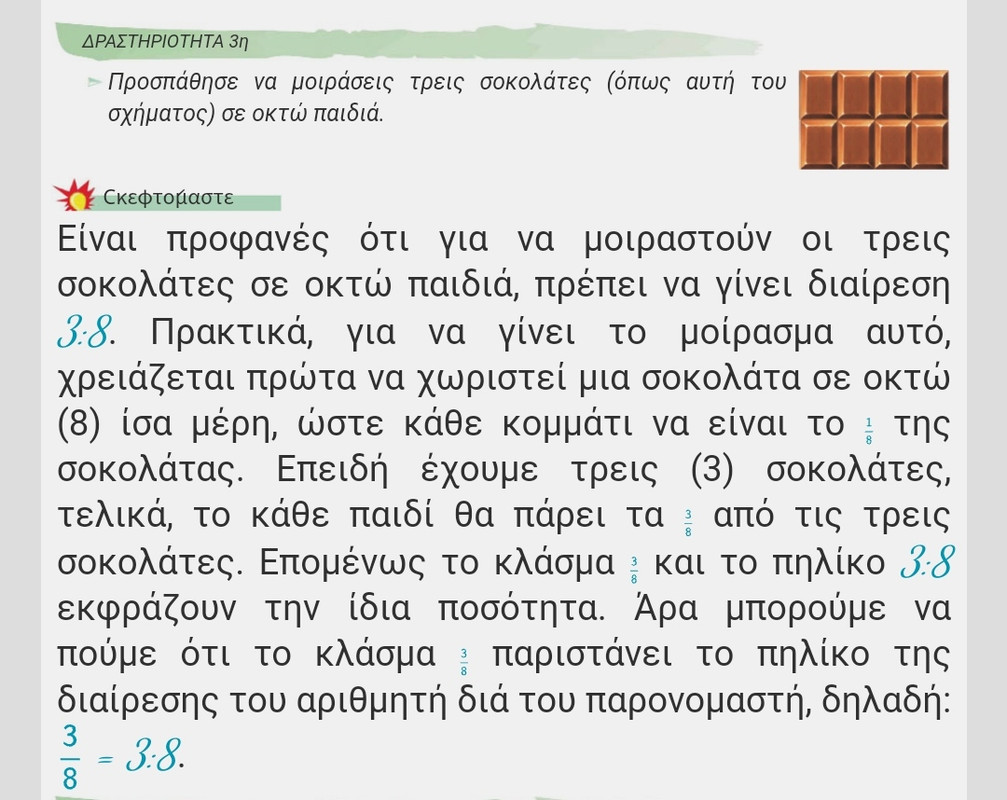
Πάμε τώρα και στην άσκηση με τις σοκολάτες. Σηκώνει η κυρία ένα παιδί στην έδρα, του δίνει τις 3 σοκολάτες (με 8 κομματάκια ή κάθε μία) και του ζητάει να ξεχωρίσει τα 3/8 των σοκολατών.
Αν αυτό γίνει ως συνέχεια του προβλήματος που συζητούσαμε σε άλλες σελίδες, το παιδί μάλλον θα ξεχωρίσει 3 μικρά κομματάκια. Αν όμως γίνει μια άλλη μέρα με τις ίδιες σοκολάτες, μπορεί να ξεχωρίσει 9 κομμάτια (τα 3/8 της συνολικής ποσότητας).
για το γλωσσικό θέμα, το πρόβλημα με την διατύπωση είναι ότι είναι στην καθομιλουμένη, κατανοητό ως ένα βαθμό αφού απευθύνεται σε παιδιά, και δεν ακριβολογεί παραλείποντας με λάθος τρόπο τα (υποτίθεται) ευκόλως εννοούμενα.
η φράση ότι κάποιος πήρε ένα αντικείμενο από ένα πλήθος αντικειμένων διαφορετικού είδους είναι:
πήρε ένα ....... από τα .......
πήρε ένα μήλο από τα φρούτα
πήρε ένα κατσαβίδι από τα εργαλεία
πήρε ένα πουκάμισο από τα ρούχα
κλπ
όταν τα αντικείμενα είναι τού ίδιου είδους η φράση γίνεται:
πήρε ένα μήλο από τα μήλα
πήρε ένα κατσαβίδι από τα κατσαβίδια
πήρε ένα πουκάμισο από τα πουκάμισα
κλπ
οπότε είτε το πρώτο είτε το δεύτερο παραλείπεται:
1. πήρε ένα μήλο (απ΄τα μήλα εννοείται, από πού αλλού να το πάρει)
2. πήρε ένα από τα μήλα (μήλο πήρε εννοείται, τι άλλο να πάρει)
στην περίπτωση τής άσκησης, όπως εξηγήσαμε, το μήλο είναι την ουσία μονάδα μέτρησης και δεν μπορεί να παραλειφθεί. αν τα μοιράζαν σε γραμμάρια θα μπορούσε η απάντηση να είναι «κάθε παιδί θα πάρει 150 από τα μήλα»;
η άσκηση όχι μόνο κάνει τις παραλείψεις, αλλά τις μπερδεύει κιόλας:
- στην εκφώνηση χρησιμοποιεί την 2η παράλειψη: «τι μέρος από τα φρούτα θα πάρει»
- στην μεθ. α χρησιμοποιεί την 1η παράλειψη, αλλά παραλείπει και τον προσδιορισμό: «θα πάρει 6/5 [τού μήλου]»
- στην μεθ. β χρησιμοποιεί πάλι την 2η παράλειψη, αλλά πετάει και λάθος γενική θέλοντας να πει «[εκ] των» αντί για «από τα»: «θα πάρει 6/5 [εκ] τών μήλων»
κανονικά δεν έπρεπε να παραλείψει τίποτα: «τι μέρος τού μήλου θα πάρει από τα μήλα κάθε παιδί;»
ή ακόμα καλύτερα να το σπάσει σε δύο σκέλη για να είναι πιο κατανοητό και να αποφεύγονται τα φαινόμενα Γκερ.
«τι μέρος τών μήλων θα πάρει κάθε παιδί; σε τι μέρος τού μήλου αντιστοιχεί αυτό;»
α) πρώτα εξηγούμε ότι για να τα μοιράσουμε θα τα χωρίσουμε σε πέντε ίσα μέρη και κάθε παιδί θα πάρει ένα από αυτά, δηλαδή κάθε παιδί θα πάρει το ένα πέμπτο (1/5) τών μήλων.
β) μετά εξηγούμε με τα κομματάκια πώς μπορούμε να καταφέρουμε να τα χωρίσουμε σε 5 ίσα μέρη με βάση το μέρος τού μήλου, ώστε κάθε παιδί να πάρει μετρημένα έξι πέμπτα (6/5) τού μήλου.
γ) τέλος εξηγούμε ότι είναι ακριβώς το ίδιο να κάνεις απ'ευθείας την διαίρεση με τον αριθμό τών παιδιών για να βρείς τι μέρος των μήλων και πόσα μήλα θα πάρει κάθε παιδί: «κάθε παιδί θα πάρει το 1/5 τών μήλων που αντιστοιχεί σε 6/5 τού μήλου (6/5 μήλα), δηλαδή κάθε παιδί θα πάρει ένα ολόκληρο μήλο και ένα πέμπτο τού μήλου (1+1/5 μήλα).»
δ) ο καλός δάσκαλος μπορεί να κάνει και λίγο εξωβιβλιακή πλακίτσα, ότι έτσι μπορούν να καταλάβουν ότι δεν είναι ανάγκη να κόψουν όλα τα μήλα για να τα μοιραστούν, αλλά μόνο ένα, οπότε δεν είναι εντελώς άχρηστα τα μαθηματικά στην ζωή.
ετσι ακριβως θα ηταν μια καλη ασκηση, και ενας καλος εκπαιδευτικος.